本記事では、コンデンサー1個と抵抗1個で完結するローパス・フィルタ回路とハイパス・フィルタ回路について紹介する。
いずれも電子回路の中で最もシンプルなフィルタ回路である。
RCローパス・フィルタ回路およびRCハイパスフィルタ回路
フィルタ回路の特性は増幅率(=Vout/Vin)と位相で決定づけられ、いずれも入力信号の周波数に依存する。
RCローパス・フィルタ回路

こういう時に使う
・入力信号の低周波成分を抽出したい。
・入力信号の高周波成分を減衰させたい。
増幅率
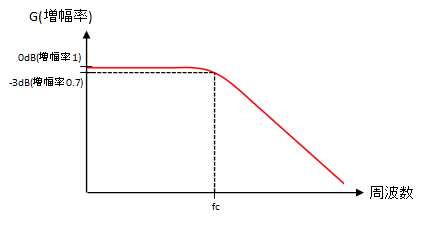
ローパスなので入力信号が低周波だと増幅率1で素通りし、高周波になると減衰していく。
位相
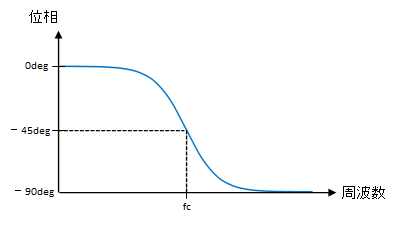
低周波では入力-出力間で位相のズレはないが、高周波になると出力側の位相が遅れはじめ、最終的に90°遅れる。
RCハイパス・フィルタ回路

こういう時に使う
・入力信号の低周波成分を減衰させたい。
・入力信号の高周波成分を抽出したい。
増幅率
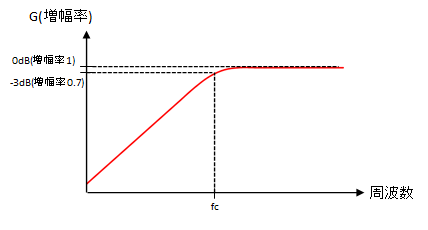
ハイパスなので入力信号が低周波だと増幅率も低く、高周波になると増幅率が上がって最終的に1になる。
位相
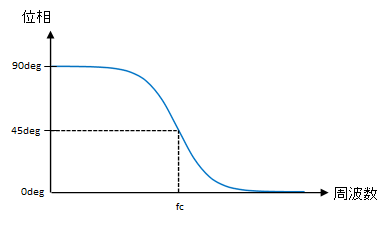
低周波では出力側の位相が90°進んでいるが、高周波になると入力-出力間の位相のズレが小さくなり、最終的にズレが無くなる。
回路図の通り、両者の違いは抵抗とコンデンサーの配置のみである。
増幅率は通常ゲイン(利得)と呼ばれる量で表される。
ゲインの定義式は下記の通り。
\begin{align}
G[\text{dB}]=20\log_{10}\left|\frac{V_{\text{out}}}{V_{\text{in}}}\right| \tag{1}\label{gain}
\end{align}
定義式に則ると、増幅率1のときにゲインが0であり、増幅も減衰もしない場合を基準とすることができる。
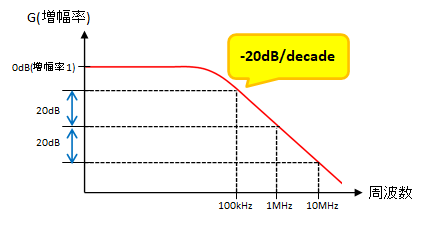
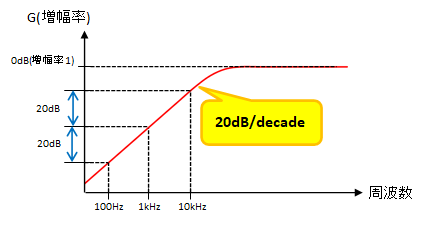
今回のフィルタ回路のゲインのグラフを見ると、RCローパス・フィルタ回路では高周波になるに連れて、RCハイパス・フィルタ回路では低周波になるに連れてゲインが直線的(リニア)に低下している。
グラフの横軸は対数目盛になっており、この傾きはちょうど±20dB/decadeとなる。
/decadeとは「桁が1つ変わると」と解釈する。
すなわちRCローパス・フィルタ回路の場合は、例えば周波数が100kHzから1MHz(1000kHz)に上がる、または1MHzから10MHzに上がるなど桁が1つ上がると、ゲインが20dB下がる。
逆にRCハイパス・フィルタ回路の場合は、例えば周波数が100Hzから1kHz(1000Hz)に上がる、または1kHzから10kHzに上がるなど桁が1つ上がると、ゲインが20dB上がる。
また、回路を特徴づける重要なパラメータにカットオフ周波数\(f_{c}\)というものがある。
カットオフ周波数は下式で定義される。
\begin{align}
f_{c}=\frac{1}{2\pi RC} \tag{2}\label{fc}
\end{align}
RCローパス・フィルタとRCハイパス・フィルタにおいては、ゲインがちょうど-3dB(増幅率だとおよそ0.7)になる周波数がカットオフ周波数である。
またこのとき、出力の位相はRCローパス・フィルタでは入力より45°遅れ、RCハイパス・フィルタでは入力より45°進んでいる。
例
ここで例題を使って具体的な回路を考えてみる。
例題
抵抗値\(R=10\Omega\)の抵抗を用いたRCローパス・フィルタ回路を考える。
このとき、次の問いに答えよ。
(1) カットオフ周波数が\(2\text{kHz}\)となるとき、コンデンサーの容量を求めよ。
(2) 周波数が\(30\text{kHz}\)のときゲインが\(-23.6\text{dB}\)となる。このとき、\(3\text{MHz}\)でのゲインを求めよ。
解説
(1)
求めるコンデンサーの容量を\(C\)とすると(\ref{gain})を変形して
\begin{align}
C&=\frac{1}{2\pi R f_{c}}=\frac{1}{2\pi \times 10\Omega \times 2\text{kHz}}=\boxed{8.0\text{μF}}
\end{align}
となる。
(2)
ゲインは周波数に対して\(-20\text{dB/decade}\)の割合で減衰する。
周波数が\(30\text{kHz}\)のときゲインが\(-23.6\text{dB}\)であるため、2桁大きい\(3\text{MHz}\)では\(-20\text{dB}\times 2=-40\text{dB}\)減衰する。
よって、求めるゲインは\(-23.6\text{dB}-40\text{dB}=\boxed{-63.6\text{dB}}\)となる。
終わりに
最近サボり癖がついていてヤバい。
できれば1つ、今年6月中にやってしまいたいことがあるが、間に合うのか…
END




コメント