力学問題第2問は、単振動と運動量保存則のコラボレーション問題だ。
問題
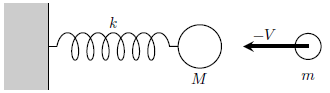
壁からばね定数\(k>0\)のばねが垂直に立っており、その先端に質量\(M\)の球1が取り付けられている。
ばねが自然長で静止しているとき、質量\(M\)の球2が速度\(-V\)で完全弾性衝突した。
ただし\(m<M\)であり、両者は質点で空気抵抗と重力は考慮しないものとする。
また図の右向きを正とする。
(a) 球1の初期位置を\(x=0\)として、衝突後の球1の運動を、縦軸を変位\(x(t)\)、横軸を時間\(t\)のグラフで示せ。
(b) 衝突後、球1が再び\(x=0\)に到達したところで、球2を再び同じ速度\(-V\)で衝突させた。この2回目の衝突後の球1の運動を、(a)で得たグラフに続けて示せ。
解答 (a)
衝突後、球1に外力を加えるのはばねのみである。よって時間を\(t\)とすると運動方程式は
\begin{align}
M\frac{d^{2}x}{dt^{2}}=-kx \tag{1}\label{1}
\end{align}
と書ける。(\ref{1})は二階の常微分方程式であり、その一般解は任意定数を\(A_{1},B_{1}\)として、
\begin{align}
x(t)=A_{1}\cos(\omega t)+B_{1}\sin(\omega t) \tag{2}\label{2}
\end{align}
となる。ただし\(\omega=\sqrt{k/M}\)である。
この2つの任意定数\(A_{1},B_{1}\)を求めることができれば球1の運動を記述できる。任意定数を求める際に使うのは初期条件(束縛条件)である。初期位置は\(x=0\)であるため、
\begin{gather}
x(0)=A_{1}\cos(\omega\times 0)+B_{1}\sin(\omega\times 0) \\
x(0)=A_{1}=0 \tag{3}\label{3}
\end{gather}
となり、\(A_{1}=0\)であることがわかる。続いて\(B_{1}\)だが、これは初速度を使って求める。変位を時間で微分すれば速度になるため、球1の速度\(v(t)\)は
\begin{align}
v(t)=\frac{dx(t)}{dt}=B_{1}\omega\cos(\omega t) \tag{4}\label{4}
\end{align}
となる。ただし\(A_{1}=0\)を利用した。よって(\ref{4})に\(t=0\)を代入すれば
\begin{align}
v(0)=B_{1}\omega\cos(\omega\times 0)=B_{1}\omega \tag{5}\label{5}
\end{align}
となり\(B_{1}=v(0)/\omega\)であることがわかる。
後は初速度\(v(0)\)を求めればよい。初速度\(v(0)\)は運動量保存則と反発係数の定義式から求められる。衝突後の球2の速度を\(v_{m}\)とすると、
\begin{gather}
M\cdot 0+m(-V)=Mv(0)+mv_{m} \tag{6}\label{6} \\
1=-\frac{v(0)-v_{m}}{0-(-V)} \tag{7}\label{7}
\end{gather}
が成立する。(\ref{6})と(\ref{7})は連立方程式であり、これを\(v(0)\)について解くと
\begin{align}
v(0)=-\frac{2m}{m+M}V \tag{8}\label{8}
\end{align}
となる。よって(\ref{8})より
\begin{align}
B_{1}=-\frac{2m}{(m+M)\omega}V \tag{9}
\end{align}
と求められる。
以上より、球1の変位はおよび速度は
\begin{align}
x(t)&=-\frac{2mV}{m+M}\sqrt{\frac{M}{k}}\sin\left(\sqrt{\frac{k}{M}}t\right) \tag{10}\label{10} \\
v(t)&=-\frac{2mV}{m+M}\cos\left(\sqrt{\frac{k}{M}}t\right) \tag{11}\label{11}
\end{align}
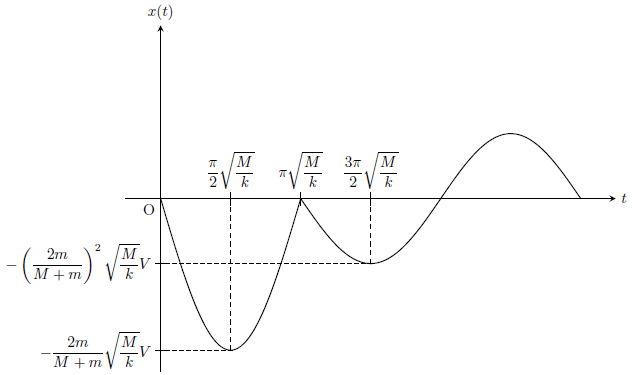
と求められ、(\ref{10})をグラフ化すると下図のようになる。

解答 (b)
基本的にやることは(a)と同じだが、初速度が異なることに注意が必要である。
(a)の運動後に球1が再び\(x=0\)を通過するのは\(t=t_{1}=\pi\sqrt{M/k}\)のときであるため、2回目の衝突直前の球1の速度は(\ref{11})より
\begin{align}
v(t_{1})=\frac{2m}{m+M}V \tag{12}\label{12}
\end{align}
となる。これを利用すると、2回目の衝突直後の球1と球2の速度をそれぞれ\(v’_{M},v’_{m}\)として、運動量保存則と反発係数の定義式より
\begin{gather}
Mv(t_{1})+m(-V)=Mv’_{M}+mv’_{m} \tag{13}\label{13} \\
1=-\frac{v’_{M}-v’_{m} }{v(t_{1})-(-V)} \tag{14}\label{14}
\end{gather}
が成立する。これらを\(v’_{M}\)について解くと、
\begin{align}
v’_{M}=-\left(\frac{2m}{m+M}\right)^{2}V \tag{15}\label{15}
\end{align}
となる。
運動方程式は(\ref{1})と同じであるため、任意定数を\(A_{2},B_{2}\)と置くと、球1の変位と速度は
\begin{align}
x(t)&=A_{2}\cos(\omega t)+B_{2}\sin(\omega t) \tag{16}\label{16} \\
v(t)&=\frac{d}{dt}x(t)=-A_{2}\omega\sin(\omega t)+B_{2}\omega\cos(\omega t) \tag{17}\label{17}
\end{align}
と書ける。(a)と同様に束縛条件\(x(t_{1})=0,v(t_{1})=v’_{M}\)を使て\(A_{2},B_{2}\)を求めると、
\begin{align}
A_{2}&=0 \tag{18}\label{18} \\
B_{2}&=\left(\frac{2m}{m+M}\right)^{2}\sqrt{\frac{M}{k}}V \tag{19}\label{19}
\end{align}
となる。
以上より、2回目の衝突以降の球1の変位および速度は
\begin{align}
x(t)&=\left(\frac{2m}{m+M}\right)^{2}\sqrt{\frac{M}{k}}V\sin\left(\sqrt{\frac{k}{M}}t\right) \tag{20}\label{20} \\
v(t)&=\left(\frac{2m}{m+M}\right)^{2}V\cos\left(\sqrt{\frac{k}{M}}t\right) \tag{21}\label{21}
\end{align}
と求められ、(\ref{20})をグラフ化すると下図のようになる。
最後に
高校物理では「ばねの単振動の角周波数は\(\sqrt{k/m}\)、単振り子の角周波数は\(\sqrt{g/\ell}\)」と丸暗記させられていた。
高校時代の先生は
「ばねは『下からミカン(\(k/m\))』、単振り子は『下からリンゴ(\(g/\ell\))』と覚えなさい」
と教わったけど、結局「上からだっけ、下からだっけ?」とそこから迷ってしまい、役に立った経験がない。
初めて微分方程式で単振動の問題を解いたときに
「もう角周波数の中身まで覚える必要ないんだ!」
と感動したものだ。
(というか実際は次元計算が身につけば、それでもう自力で角周波数だけ導けるんだけど。)
とりあえず力学の問題解説は一旦ここで区切りをつけようと思う。
また面白い問題、よくできている問題があったら順次解説していきたい。
END




コメント