教師なし学習の1つのクラスタリングについて
から解説してきた。
今回はそのクラスタリングとともに、教師なし学習の代表格である「次元削減」について扱う。
次元削減
ここでいう次元削減とは、分類問題におけるカテゴリーを決定づける特徴量の種類の数を減らすことである。
例えば下の表のように、\(X_{1}~X_{5}\)という5つの特徴量が決まると、\(Y=0,1,2\)のいずれかのカテゴリーに振り分けられるデータ群が存在するとする。
この5次元の情報をなるべく維持したまま、5次元よりも低次の次元に落とすのが次元削減だ。
| \(X_{1}\) | \(X_{2}\) | \(X_{3}\) | \(X_{4}\) | \(X_{5}\) | \(Y\) |
| 1 | 0.2 | -2 | 30 | 200 | 0 |
| 4 | 0.5 | -5 | 50 | 300 | 1 |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 7 | 0.7 | -7 | 80 | 700 | 2 |
↓
| \(X’_{1}\) | \(X’_{2}\) | \(Y\) |
| -0.24 | -0.21 | 0 |
| -0.03 | 0.08 | 1 |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 1.1 | 0.03 | 2 |
上の例では、5次元から2次元への次元削減を示している。
2次元、ないしは3次元まで削減することでグラフによる分類の可視化が可能になる。
次元削減をすることにより得られる特徴量は、最初の特徴量とは全く別物になっていることに注意。
利用場面例
具体的な例を挙げて、もう少しイメージしやすい解説を試みる。
例えば多くの不動産に関するデータがあり、その中に「建築面積」と「敷地面積」のデータがあったとする。
「建築面積」とは一般的には「建物の1階部分の面積」であり、「敷地面積」は「建物がある土地全体の面積」である。
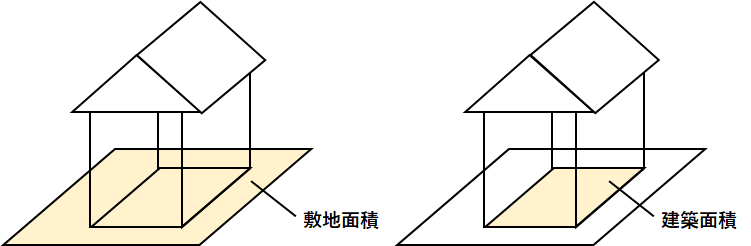
素直に考えると、「敷地面積」が大きければ「建築面積」も大きくなる、すなわちこの2つのデータの間には正の相関があると予想できる。
そして実際に、両者には正の相関が見られた場合は、傾きの方向に軸を取ってデータを圧縮して新たなパラメータを得る。
今回の場合は新たなパラメータを「広さ」と名付けても良いだろう。
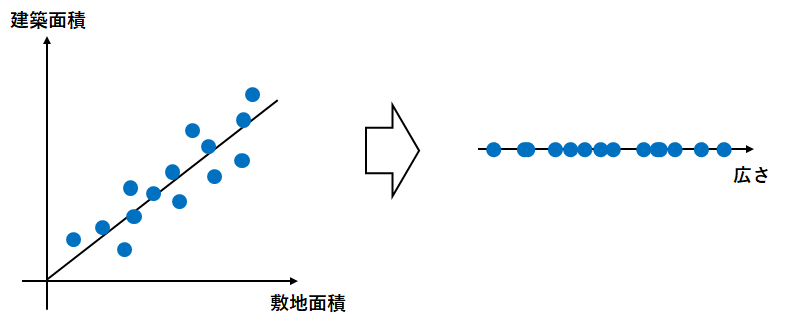
結果、「敷地面積」と「建築面積」という2つのパラメータを「広さ」という1つのパラメータに削減することが出来た。
パラメータ数が少ないほどモデル構築が楽になるため、パラメータ数が多いモデルに対してはこのようにパラメータ間の相関の有無を調べ、特に相関が強いパラメータをまとめるのが有効な策となり得る。
実装例
今回は次元削減の主な手法である主成分分析(PCA)を用いた上で、ロジスティック回帰で実際に分類を実行するプログラムを書いてみた。
実装例
# モジュールのインポート
import pandas as pd
import sklearn
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# データセットのインポート
file=pd.read_csv('PCA.csv')
# データの割り振り
X=file.iloc[:,0:5]
Y=file.iloc[:,5]
# データセットを学習データ(8割)とテストデータ(2割)に分割(random_stateは0)
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)
# 分割の確認
print('分割の確認:',X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
# 標準化のためのインスタンス作成
std=StandardScaler()
# 標準化
X_train_std=std.fit_transform(X_train)
X_test_std=std.transform(X_test)
# 主成分分析のためのインスタンス作成
pca=PCA(n_components=2)
# 次元削減
X_train_pca=pca.fit_transform(X_train_std)
X_test_pca=pca.transform(X_test_std)
# 次元削減後のデータ数確認
print('次元削減後:',X_train_pca.shape, X_test_pca.shape, Y_train.shape, Y_test.shape)
# 学習実行
# ロジスティック回帰のインスタンスの作成
model=LogisticRegression(max_iter=1000)
# モデルの作成
model.fit(X_train_pca,Y_train)
# 学習データからの予測値
pred_train = model.predict(X_train_pca)
# テストデータからの予測値
pred_test = model.predict(X_test_pca)
# 学習データを用いた分類モデルの評価
print('正解率(学習データ) = ', metrics.accuracy_score(Y_train, pred_train))
# テストデータを用いた分類モデルの評価
print('正解率(テストデータ) = ', metrics.accuracy_score(Y_test, pred_test))出力例
分割の確認: (80, 5) (20, 5) (80,) (20,)
次元削減後: (80, 2) (20, 2) (80,) (20,)
正解率(学習データ) = 1.0
正解率(テストデータ) = 1.0実際にプログラムを実行したい場合は、下記ボタンよりcsvファイル「PCA.csv」をダウンロードしてプログラムの保存先に保存すること。
コード詳説
いくつかはロジスティック回帰のプログラム例の流用なので、下記を参照。
# 標準化のためのインスタンス作成
std=StandardScaler()
# 標準化
X_train_std=std.fit_transform(X_train)
X_test_std=std.transform(X_test)⇒主成分分析の準備として、特徴量の標準化を実施するコード。
「標準化」とは平均0、分散1のデータ群に変換する操作であり、これにより特徴量のスケール(値の大きさ)を揃える。
# 主成分分析のためのインスタンス作成
pca=PCA(n_components=2)
# 次元削減
X_train_pca=pca.fit_transform(X_train_std)
X_test_pca=pca.transform(X_test_std)
# 次元削減後のデータ数確認
print('次元削減後:',X_train_pca.shape, X_test_pca.shape, Y_train.shape, Y_test.shape)⇒標準化した特徴量に対して主成分分析(次元削減)を実行し、データの構造を確認するためのコード。
「n_components」は落とす次元数を指定するコードであり、今回は2次元まで落とすように設定している。
コードを実行すると、実際に特徴量の種類の数が5から2に減っていることを確認できる。
次元削減後: (80, 2) (20, 2) (80,) (20,)終わりに
これで教師あり学習、教師なし学習を含め、機械学習の代表的なアルゴリズムを取り上げ切ったつもりだ。
記事的にはまだまだ粗削りな部分があるため、今後は記事の改善、加えてアルゴリズムの詳細説明まで深堀りしたいと思う。
一回本を吟味してちゃんと勉強したほうが良いな…
参考文献
私が受講した通信講座。
機械学習とはなんぞやという体系的な話からPython操作の基礎、各アルゴリズムの理論、プログラムの実装例まで取り上げ、短期間で最低限の実用レベルまで学ぶことができるようになっている。
最低限の知識で全体を俯瞰しながら実装レベルまで学びたかった私にとって、最適な「足掛かり」となる講座だった。
END





コメント