下記2記事にて、線積分と面積分を扱った。
今回はその応用として、線積分と面積分の関係を表した定理であるストークスの定理を扱う。
概要
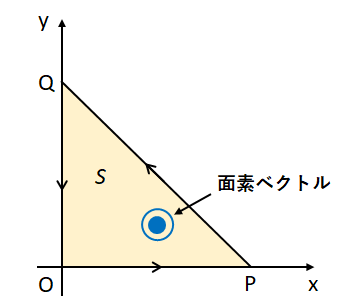
ある閉じた経路\(C\)があり、\(C\)を縁とする面を\(S\)とする。
このとき、あるベクトル場\(\vec{A}\)をこの経路\(C\)に沿って線積分した結果は、ベクトル場\(\vec{A}\)の回転を面\(S\)で面積分した結果に等しくなる。
\begin{align}
\int_{C}\vec{A}\cdot d\vec{r}=\iint_{S}\text{rot}\vec{A}\cdot d\vec{S}
\end{align}
これがストークスの定理である。
面素ベクトルの向きは、経路\(C\)の正の方向に対して右ねじの進行方向にとる。
実用例としては電磁気学での、ファラデーの電磁誘導の法則の微分形から積分形(またはその逆)への変形が挙げられる(下記記事参照)。
例題1
例題1
原点O:\((0,0,0)\)、点P:\((1,0,0)\)、点Q:\((0,1,0)\)の3点をつないだ経路を\(C\)とし、経路\(C\)を縁とするx-y平面内の平面を\(S\)とする。
また、\(a\)を定数としてベクトル場\(\vec{A}=(-ay,ax,0)\)を考える。
このとき、次の問いに答えよ。
(1) 経路\(C\)に沿った\(\vec{A}\)の線積分を求めよ。ただし、線積分の向きは図1の矢印の方向(反時計方向)にとる。
(2) 平面\(S\)上での\(\text{rot}\vec{A}\)の面積分を求めよ。

解説
(1)
経路\(C\)は3本の線分から構成されているため、各線分の線積分を計算して足し上げればよい。
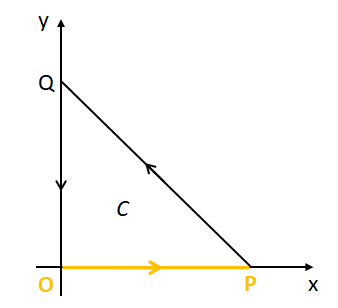
(i) 線分OP上での線積分
線分OP上での位置ベクトルは変数\(t\)を使って\(\vec{r}_{1}=(t,0,0)\)と書けるため、線素ベクトル\(d\vec{r}_{1}\)は
\begin{align}
d\vec{r}_{1}=dt\frac{d\vec{r}_{1}}{dt}=dt(1,0,0) \tag{1}\label{stokesrei1-1-1}
\end{align}
となる。
また位置ベクトル\(\vec{r}_{1}\)をベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(0,at,0) \tag{2}\label{stokesrei1-1-2}
\end{align}
となる。
\(\vec{A}\)と\(d\vec{r}_{1}\)の内積を取ると0になるため、線積分も0になる。
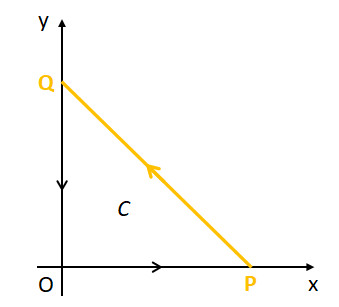
(ii) 線分PQ上での線積分
線分PQ上での位置ベクトルは変数\(t\)を使って\(\vec{r}_{2}=(t,-t+1,0)\)と書けるため、線素ベクトル\(d\vec{r}_{2}\)は
\begin{align}
d\vec{r}_{2}=dt\frac{d\vec{r}_{2}}{dt}=dt(1,-1,0) \tag{3}\label{stokesrei1-1-3}
\end{align}
となる。
また位置ベクトル\(\vec{r}_{2}\)をベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(-a(-t+1),at,0)=(a(t-1),at,0) \tag{4}\label{stokesrei1-1-4}
\end{align}
となる。
よって線分PQ上での線積分は(\ref{stokesrei1-1-3})と(\ref{stokesrei1-1-4})より
\begin{align}
\int_{PQ}\vec{A}\cdot d\vec{r}_{2}&=\int_{PQ}(a(t-1),at,0)\cdot dt(1,-1,0) \notag \\
&=\int_{1}^{0}\{a(t-1)-at\}dt \notag \\
&=-a\int_{1}^{0}dt=a \tag{5}
\end{align}
となる。
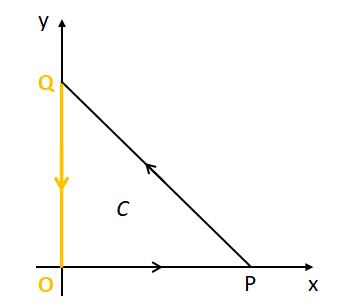
(iii) 線分QO上での線積分
線分QO上での位置ベクトルは変数\(t\)を使って\(\vec{r}_{3}=(0,t,0)\)と書けるため、線素ベクトル\(d\vec{r}_{3}\)は
\begin{align}
d\vec{r}_{3}=dt\frac{d\vec{r}_{3}}{dt}=dt(0,1,0) \tag{6}\label{stokesrei1-1-5}
\end{align}
となる。
また位置ベクトル\(\vec{r}_{3}\)をベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(-at,0,0) \tag{7}\label{stokesrei1-1-6}
\end{align}
となる。
\(\vec{A}\)と\(d\vec{r}_{3}\)の内積を取ると0になるため、線積分も0になる。
以上より、求める線積分は(i)~(iii)より
\begin{align}
\int_{C}\vec{A}\cdot d\vec{r}=0+a+0=\boxed{a} \tag{8}
\end{align}
となる。
(2)
まず\(\text{rot}\vec{A}\)を計算する。
\begin{align}
&\text{rot}\vec{A} \notag \\
=&\nabla\times(-ay,ax,0) \notag \\
=&\left(-\frac{\partial}{\partial z}ax,\frac{\partial}{\partial z}(-ay),\frac{\partial}{\partial x}ax-\frac{\partial}{\partial y}(-ay)\right) \notag \\
=&(0,0,2a)\tag{9}\label{stokesrei1-2-1}
\end{align}
面\(S\)における面素ベクトル\(d\vec{S}\)は経路\(C\)の向きから\(d\vec{S}=(0,0,1)dS\)となる。
よって、求める面積分は(\ref{stokesrei1-2-1})より
\begin{align}
\iint_{S}\text{rot}\vec{A}\cdot d\vec{S}&=\iint_{S}(0,0,2a)\cdot (0,0,1)dS \notag \\
&=2a\iint_{S}dS=2a\cdot\frac{1}{2}=\boxed{a} \tag{10}
\end{align}
となる。
例題2
例題2
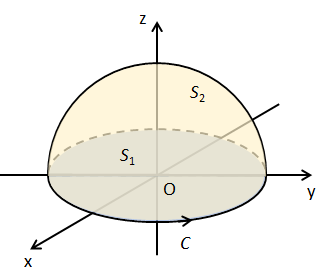
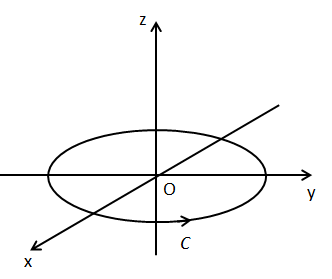
図2のように原点O:\((0,0,0)\)を中心とする半径\(R\)の円を\(C\)とする。
また、\(a,b\)を定数としてベクトル場\(\vec{A}=(ay,bx,0)\)を考える。
このとき、次の問いに答えよ。
(1) 円\(C\)に沿った\(\vec{A}\)の線積分を求めよ。ただし線積分の向きは図2の矢印の方向にとる。
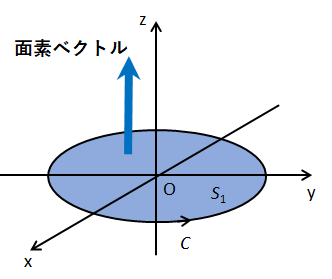
(2) 円\(C\)を縁とするx-y平面内の平面\(x^{2}+y^{2}\leq R^{2}\)を\(S_{1}\)とする。このとき、平面\(S_{1}\)上での\(\text{rot}\vec{A}\)の面積分を求めよ。
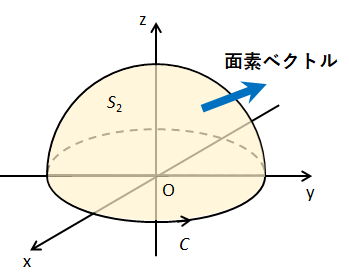
(3) 半径\(R\)の半球\(x^{2}+y^{2}+z^{2}=R^{2},z\geq 0\)の表面を\(S_{2}\)とする。このとき、球面\(S_{2}\)上での\(\text{rot}\vec{A}\)の面積分を求めよ。
解説
(1)
円\(C\)上での位置ベクトルは変数\(\theta\)を使って\(\vec{r}=(R\cos\theta,R\sin\theta,0)\)と書けるため、線素ベクトル\(d\vec{r}\)は
\begin{align}
d\vec{r}=d\theta\frac{d\vec{r}}{d\theta}=d\theta(-R\sin\theta,R\cos\theta,0) \tag{11}\label{stokesrei2-1-1}
\end{align}
となる。
また位置ベクトル\(\vec{r}\)をベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(aR\sin\theta,bR\cos\theta,0) \tag{12}\label{stokesrei2-1-2}
\end{align}
となる。
よって経路\(C\)上での線積分は(\ref{stokesrei2-1-1})と(\ref{stokesrei2-1-2})より
\begin{align}
\int_{C}\vec{A}\cdot d\vec{r}&=\int_{C}(aR\sin\theta,bR\cos\theta,0)\cdot d\theta(-R\sin\theta,R\cos\theta,0) \notag \\
&=R^{2}\int_{0}^{2\pi}(b\cos^{2}\theta-a\sin^{2}\theta)d\theta \notag \\
&=R^{2}\int_{0}^{2\pi}\left\{\frac{b}{2}(1+\cos2\theta)-\frac{a}{2}(1-\cos2\theta)\right\}d\theta \notag \\
&=R^{2}\left[\frac{b}{2}\left(\theta+\frac{1}{2}\sin2\theta\right)-\frac{a}{2}\left(\theta-\frac{1}{2}\sin2\theta\right)\right]_{0}^{2\pi} \notag \\
&=\boxed{\pi R^{2}(b-a)} \tag{13}
\end{align}
となる。
(2)
まず\(\text{rot}\vec{A}\)を計算する。
\begin{align}
&\text{rot}\vec{A} \notag \\
=&\nabla\times(ay,bx,0) \notag \\
=&\left(-\frac{\partial}{\partial z}bx,\frac{\partial}{\partial z}ay,\frac{\partial}{\partial x}bx-\frac{\partial}{\partial y}ay\right) \notag \\
=&(0,0,b-a)\tag{14}\label{stokesrei2-2-1}
\end{align}
面\(S_{1}\)における面素ベクトル\(d\vec{S_{1}}\)は経路\(C\)の向きから\(d\vec{S_{1}}=(0,0,1)dS_{1}\)となる。
よって、求める面積分は(\ref{stokesrei2-2-1})より
\begin{align}
\iint_{S_{1}}\text{rot}\vec{A}\cdot d\vec{S_{1}}&=\iint_{S_{1}}(0,0,b-a)\cdot (0,0,1)dS_{1} \notag \\
&=(b-a)\iint_{S_{1}}dS_{1}=2a\cdot\pi R^{2}=\boxed{\pi R^{2}(b-a)} \tag{15}
\end{align}
となる。
(3)
\(\text{rot}\vec{A}\)は(\ref{stokesrei2-2-1})より
\begin{align}
\text{rot}\vec{A}=(0,0,b-a)\tag{16}\label{stokesrei2-3-1}
\end{align}
となる。
面\(S_{2}\)における面素ベクトル\(d\vec{S_{2}}\)の向きは、経路\(C\)の向きから球から外向きになる。
下記記事
の結果を利用すると、面素ベクトル\(d\vec{S}_{2}\)は極座標表示を用いて
\begin{align}
d\vec{S}_{2}=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)R^{2}\sin\theta d\theta d\phi \tag{17}\label{stokesrei2-3-2}
\end{align}
となる。
よって、求める面積分は(\ref{stokesrei2-3-1})と(\ref{stokesrei2-3-2})より
\begin{align}
\iint_{S_{2}}\text{rot}\vec{A}\cdot d\vec{S_{2}}&=\iint_{S_{2}}(0,0,b-a)\cdot(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)R^{2}\sin\theta d\theta d\phi \notag \\
&=R^{2}(b-a)\int_{0}^{\pi/2}d\theta\int_{0}^{2\pi}d\phi\,\sin\theta\cos\theta \notag \\
&=\frac{R^{2}(b-a)}{2}\left(\int_{0}^{\pi/2}\sin2\theta\,d\theta\right)\left(\int_{0}^{2\pi}d\phi\right) \notag \\
&=\frac{R^{2}(b-a)}{2}\left[-\frac{1}{2}\cos2\theta\right]_{0}^{\pi/2}\cdot 2\pi \notag \\
&=\boxed{\pi R^{2}(b-a)} \tag{18}
\end{align}
となる。
積分対象が半球面なので\(\theta\)の範囲が\(0\leq\theta\leq\pi/2\)となることに注意。
終わりに
ストークスの定理に関してはここで締める。
次回、面積分と体積積分の関係を示したガウスの定理を扱って、ベクトル解析の記事は一旦区切りをつけようと思う。
END





コメント