前回
にて、ベクトル解析において重要な定理であるストークスの定理を扱った。
今回も、ベクトル解析にて登場する重要な積分定理の1つであるガウスの定理を見ていく。
概要
ある閉曲面\(S\)があり、\(S\)に囲まれた有限の領域を\(V\)とする。
このとき、あるベクトル場\(\vec{A}\)をこの閉曲面\(S\)上で面積分した結果は、ベクトル場\(\vec{A}\)の発散を領域\(V\)で体積積分した結果に等しくなる。
\begin{align}
\iint_{S}\vec{A}\cdot d\vec{S}=\iiint_{V}\text{div}\vec{A}\cdot dV
\end{align}
これがガウスの定理(ガウスの発散定理)である。
面素ベクトルの向きは、閉曲面に対して外向きにとる。
実用例としては電磁気学での、ガウスの法則の微分形から積分形(またはその逆)への変形が挙げられる(下記記事参照)。
「ガウスの法則」は電磁気学で登場する物理法則であり、数学の積分定理である「ガウスの定理」とは異なるので混同しないように注意すること。
例題1
例題1
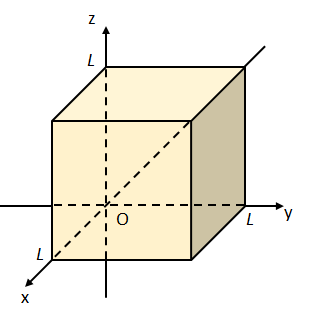
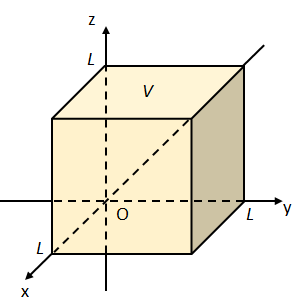
図1のようにデカルト座標系に配置された一辺の長さが\(L\)の立方体を\(V\)とし、立方体\(V\)の表面を\(S\)とする。
また、ベクトル場\(\vec{A}=(2xz,xy,-yz)\)を考える。
このとき、次の問いに答えよ。
(1) 表面\(S\)での\(\vec{A}\)の面積分を求めよ。
(2) 立方体\(V\)での\(\text{div}\vec{A}\)の体積積分を求めよ。
解説
(1)
立方体を構成する各面に対して面積分を計算し、最後に全て足し上げる。
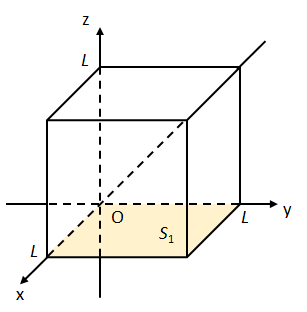
(i) 面\(S_{1}:0\leq x\leq L,0\leq y\leq L,z=0\)について
面の微小領域に法線ベクトルをかけたものが面素ベクトルになる。
面素ベクトルの向きは立方体に対して外向きになるため、面素ベクトル\(d\vec{S}_{1}\)は
\begin{align}
d\vec{S}_{1}=(0,0,-1)dxdy \tag{1}\label{gaussteiri1-1-1-1}
\end{align}
となる。
面\(S_{1}\)内の位置ベクトルを\(\vec{r}_{1}\)とすると\(\vec{r}_{1}=(x,y,0)\)となるため、これをベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(0,xy,0) \tag{2}\label{gaussteiri1-1-1-2}
\end{align}
となる。
\(\vec{A}\)と\(d\vec{S}_{1}\)の内積を取ると0になるため、面積分も0になる。
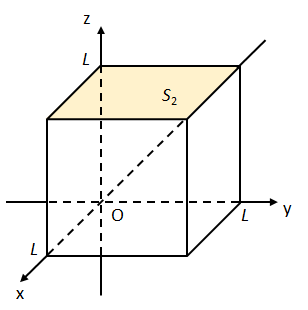
(ii) 面\(S_{2}:0\leq x\leq L,0\leq y\leq L,z=L\)について
(i)と同様に考えると、面素ベクトル\(d\vec{S}_{2}\)は
\begin{align}
d\vec{S}_{2}=(0,0,1)dxdy \tag{3}\label{gaussteiri1-1-2-1}
\end{align}
となる。
面\(S_{2}\)内の位置ベクトルを\(\vec{r}_{2}\)とすると\(\vec{r}_{2}=(x,y,L)\)となるため、これをベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(2Lx,xy,-Ly) \tag{4}\label{gaussteiri1-1-2-2}
\end{align}
となる。
よって面\(S_{2}\)上での面積分は
\begin{align}
\iint_{S_{2}}\vec{A}\cdot d\vec{S}_{2}&=\iint_{S_{2}}(2Lx,xy,-Ly)\cdot (0,0,1)dxdy \notag \\
&=\int_{0}^{L}dx\int_{0}^{L}dy(-Ly) \notag \\
&=-L\left(\int_{0}^{L}dx\right)\left(\int_{0}^{L}ydy\right) \notag \\
&=-L\cdot L\cdot \frac{L^{2}}{2}=-\frac{L^{4}}{2} \tag{5}\label{gaussteiri1-1-2-3}
\end{align}
となる。
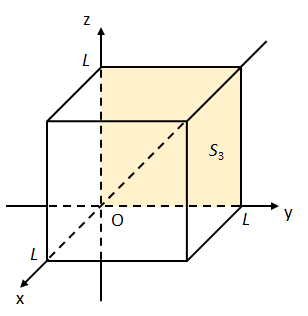
(iii) 面\(S_{3}:0\leq y\leq L,0\leq z\leq L,x=0\)について
(i)と同様に考えると、面素ベクトル\(d\vec{S}_{3}\)は
\begin{align}
d\vec{S}_{3}=(-1,0,0)dydz \tag{6}\label{gaussteiri1-1-3-1}
\end{align}
となる。
面\(S_{3}\)内の位置ベクトルを\(\vec{r}_{3}\)とすると\(\vec{r}_{3}=(0,y,z)\)となるため、これをベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(0,0,-yz) \tag{7}\label{gaussteiri1-1-3-2}
\end{align}
となる。
\(\vec{A}\)と\(d\vec{S}_{3}\)の内積を取ると0になるため、面積分も0になる。
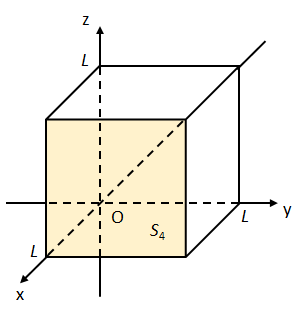
(iv) 面\(S_{4}:0\leq y\leq L,0\leq z\leq L,x=L\)について
(i)と同様に考えると、面素ベクトル\(d\vec{S}_{4}\)は
\begin{align}
d\vec{S}_{4}=(1,0,0)dydz \tag{8}\label{gaussteiri1-1-4-1}
\end{align}
となる。
面\(S_{4}\)内の位置ベクトルを\(\vec{r}_{4}\)とすると\(\vec{r}_{4}=(L,y,z)\)となるため、これをベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(2Lz,Ly,-yz) \tag{9}\label{gaussteiri1-1-4-2}
\end{align}
となる。
よって面\(S_{4}\)上での面積分は
\begin{align}
\iint_{S_{4}}\vec{A}\cdot d\vec{S}_{4}&=\iint_{S_{4}}(2Lz,Ly,-yz)\cdot (1,0,0)dydz \notag \\
&=\int_{0}^{L}dy\int_{0}^{L}dz(2Lz) \notag \\
&=2L\left(\int_{0}^{L}dy\right)\left(\int_{0}^{L}zdz\right) \notag \\
&=2L\cdot L\cdot \frac{L^{2}}{2}=L^{4} \tag{10}\label{gaussteiri1-1-4-3}
\end{align}
となる。
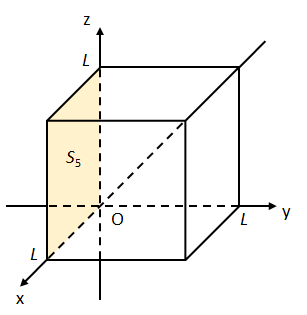
(v) 面\(S_{5}:0\leq z\leq L,0\leq x\leq L,y=0\)について
(i)と同様に考えると、面素ベクトル\(d\vec{S}_{5}\)は
\begin{align}
d\vec{S}_{5}=(0,-1,0)dzdx \tag{11}\label{gaussteiri1-1-5-1}
\end{align}
となる。
面\(S_{5}\)内の位置ベクトルを\(\vec{r}_{5}\)とすると\(\vec{r}_{5}=(x,0,z)\)となるため、これをベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(2xz,0,0) \tag{12}\label{gaussteiri1-1-5-2}
\end{align}
となる。
\(\vec{A}\)と\(d\vec{S}_{5}\)の内積を取ると0になるため、面積分も0になる。
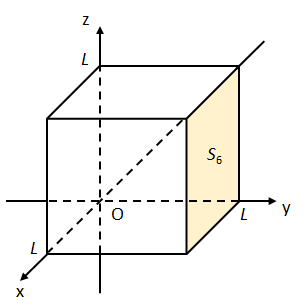
(vi) 面\(S_{6}:0\leq z\leq L,0\leq x\leq L,y=L\)について
(i)と同様に考えると、面素ベクトル\(d\vec{S}_{6}\)は
\begin{align}
d\vec{S}_{6}=(0,1,0)dzdx \tag{13}\label{gaussteiri1-1-6-1}
\end{align}
となる。
面\(S_{6}\)内の位置ベクトルを\(\vec{r}_{6}\)とすると\(\vec{r}_{6}=(x,L,z)\)となるため、これをベクトル場\(\vec{A}\)に適用すると
\begin{align}
\vec{A}=(2xz,Lx,-Lz) \tag{14}\label{gaussteiri1-1-6-2}
\end{align}
となる。
よって面\(S_{6}\)上での面積分は
\begin{align}
\iint_{S_{6}}\vec{A}\cdot d\vec{S}_{6}&=\iint_{S_{6}}(2xz,Lx,-Lz)\cdot (0,1,0)dzdx \notag \\
&=\int_{0}^{L}dz\int_{0}^{L}dx\,(Lx) \notag \\
&=L\left(\int_{0}^{L}dz\right)\left(\int_{0}^{L}xdx\right) \notag \\
&=L\cdot L\cdot \frac{L^{2}}{2}=\frac{L^{4}}{2} \tag{15}\label{gaussteiri1-1-6-3}
\end{align}
となる。
よって(i)~(vi)より求める面積分は
\begin{align}
\iint_{S}\vec{A}\cdot d\vec{S}=-\frac{L^{4}}{2}+L^{4}+\frac{L^{4}}{2}=\boxed{L^{4}} \tag{16}
\end{align}
となる。
(2)
まず\(\text{div}\vec{A}\)を計算する。
\begin{align}
\text{div}\vec{A}&=\nabla\cdot(2xz,xy,-yz) \notag \\
&=\frac{\partial}{\partial x}2xz+\frac{\partial}{\partial y}xy+\frac{\partial}{\partial z}(-yz) \notag \\
&=2z+x-y \tag{17}\label{gaussteiri1-2-1}
\end{align}
よって、求める体積積分は(\ref{gaussteiri1-2-1})より
\begin{align}
\iint_{V}\text{div}\vec{A}\,dV&=\iiint_{V}(2z+x-y)dxdydz \notag \\
&=\int_{0}^{L}dx\int_{0}^{L}dy\int_{0}^{L}dx(2z+x-y) \notag \\
&=\int_{0}^{L}dx\int_{0}^{L}dy\biggl[z^{2}+xz-yz\biggr]_{0}^{L} \notag \\
&=\int_{0}^{L}dx\int_{0}^{L}dy(L^{2}+Lx-Ly) \notag \\
&=\int_{0}^{L}dx\left[L^{2}y+Lxy-\frac{L}{2}y^{2}\right]_{0}^{L} \notag \\
&=\int_{0}^{L}dx\left(L^{3}+L^{2}x-\frac{L^{3}}{2}\right) \notag \\
&=\left[\frac{L^{3}}{2}x+\frac{L^{2}}{2}x^{2}\right]_{0}^{L}=\boxed{L^{4}} \tag{18}
\end{align}
となる。
例題2
例題2
図2のように原点Oを中心とする半径2の球を\(V\)とし、球\(V\)の表面を\(S\)とする。
また、ベクトル場\(\vec{A}=(2x,2y,2z)\)を考える。このとき、次の問いに答えよ。
(1) 表面\(S\)での\(\vec{A}\)の面積分を求めよ。
(2) 立方体\(V\)での\(\text{div}\vec{A}\)の体積積分を求めよ。
解説
(1)
まず面\(S\)上の位置ベクトル\(\vec{r}\)を2つの変数で表す。
面\(S\)は原点Oを中心とする半径2の球面であるため、位置ベクトルは極座標表示を利用して
\begin{align}
\vec{r}=(2\sin\theta\cos\phi,2\sin\theta\sin\phi,2\cos\theta)\,\quad\left(0\leq\theta\leq\pi,0\leq\phi\leq 2\pi\right) \tag{19}\label{gaussteiri2-1-2-1}
\end{align}
と書ける。
ここでこの位置ベクトル\(\vec{r}\)を\(\theta\)および\(\phi\)で偏微分すると(\ref{gaussteiri2-1-2-1})より
\begin{align}
&\frac{\partial \vec{r}}{\partial \theta}=(2\cos\theta\cos\phi,2\cos\theta\sin\phi,-2\sin\theta) \tag{20}\label{gaussteiri2-1-2-2}\\
&\frac{\partial \vec{r}}{\partial \phi}=(-2\sin\theta\sin\phi,2\sin\theta\cos\phi,0) \tag{21}\label{gaussteiri2-1-2-3}
\end{align}
となる。
次にこれら2つの偏微分の外積を取る。
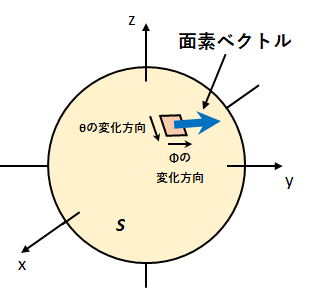
図3のように面素ベクトルの向きが球面に対して外向きであるとき、\(\theta\to\phi\)の組み合わせで面素ベクトルに対して右ねじの向きになる。
よって外積かける順番は(\(\theta\)の偏微分)\(\times\)(\(\phi\)の偏微分)となるため、(\ref{gaussteiri2-1-2-2})と(\ref{gaussteiri2-1-2-3})より
\begin{align}
\frac{\partial \vec{r}}{\partial \theta}\times\frac{\partial \vec{r}}{\partial \phi}&=(2\cos\theta\cos\phi,2\cos\theta\sin\phi,-2\sin\theta)\times(-2\sin\theta\sin\phi,2\sin\theta\cos\phi,0)\notag \\
&=(4\sin^{2}\theta\cos\phi,4\sin^{2}\theta\sin\phi,4\sin\theta\cos\theta\cos^{2}\phi+4\sin\theta\cos\theta\sin^{2}\phi) \notag \\
&=(4\sin^{2}\theta\cos\phi,4\sin^{2}\theta\sin\phi,4\sin\theta\cos\theta) \notag \\
&=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)4\sin\theta \tag{22}\label{gaussteiri2-1-2-4}
\end{align}
と計算できる。
よって面素ベクトルは\(d\vec{S}\)とすると(\ref{gaussteiri2-1-2-4})の結果を利用して
\begin{align}
d\vec{S}&=\left(\frac{\partial \vec{r}}{\partial \theta}\times\frac{\partial \vec{r}}{\partial \phi}\right)d\theta d\phi=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)4\sin\theta d\theta d\phi \tag{23}\label{gaussteiri2-1-2-5}
\end{align}
となる。
続いてベクトル場\(\vec{A}\)に位置ベクトル\(\vec{r}\)を適用すると
\begin{align}
\vec{A}&=(2\cdot 2\sin\theta\cos\phi,2\cdot 2\sin\theta\sin\phi,2\cdot 2\cos\theta)\notag \\
&=(4\sin\theta\cos\phi,4\sin\theta\sin\phi,4\cos\theta) \tag{24}\label{gaussteiri2-1-2-6}
\end{align}
となる。
よって面の範囲を考慮すると積分範囲は\(\theta:0\to\pi,\phi:0\to 2\pi\)となるため、面\(S\)上での面積分は(\ref{gaussteiri2-1-2-5})と(\ref{gaussteiri2-1-2-6})より
\begin{align}
&\iint_{S}\vec{A}\cdot d\vec{S}\notag \\
=&\iint_{S}(4\sin\theta\cos\phi,4\sin\theta\sin\phi,4\cos\theta)\cdot (\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)4\sin\theta d\theta d\phi \notag \\
=&16\int_{0}^{\pi}d\theta\int_{0}^{2\pi}d\phi\,(\sin^{2}\theta\cos^{2}\phi+\sin^{2}\theta\sin^{2}\phi+\cos^{2}\theta)\sin\theta \notag \\
=&16\left(\int_{0}^{\pi}\sin\theta\,d\theta\right)\left(\int_{0}^{2\pi}d\phi\right) \notag \\
=&16\biggl[-\cos\theta\biggr]_{0}^{\pi}\cdot 2\pi \notag \\
=&16\cdot 2\cdot 2\pi=\boxed{64\pi} \tag{25}
\end{align}
となる。
(2)
まず\(\text{div}\vec{A}\)を計算する。
\begin{align}
\text{div}\vec{A}&=\nabla\cdot(2x,2y,2z) \notag \\
&=\frac{\partial}{\partial x}2x+\frac{\partial}{\partial y}2y+\frac{\partial}{\partial z}2z \notag \\
&=6 \tag{26}\label{gaussteiri2-2-1}
\end{align}
よって、求める体積積分は(\ref{gaussteiri2-2-1})より
\begin{align}
\iint_{V}\text{div}\vec{A}\,dV&=\iiint_{V}6\,dxdydz=6\cdot\frac{4}{3}\cdot 2^{3}\pi=\boxed{64\pi} \tag{27}
\end{align}
となる。
終わりに
今回の記事で、ベクトル解析に関する記事の執筆は一旦区切りをつけることにする。
次に数学の記事を書くならフーリエ変換かラプラス変換だろうか…
いずれにしてもほぼ一から復習しないといけないレベルだから、また気が向いたときにでも勉強しようと思う。
END






コメント