前回
の続き。
今回はオペアンプを使った負帰還回路のうち基本となるボルテージフォロワ、非反転増幅回路、反転増幅回路を取り上げる。
復習
非反転増幅端子から入る電圧を\(V_\text{in}^{+}\)、反転増幅端子から入る電圧を\(V_\text{in}^{-}\)、開ループゲイン(オペアンプ特有の増幅率)を\(A\)とすると、増幅された出力電圧\(V_{\text{out}}\)は次式で表される。
\begin{align}
V_{\text{out}}=A(V_\text{in}^{+}-V_\text{in}^{-}) \label{opamp1}\tag{1}
\end{align}
またオペアンプを用いた負帰還回路の伝達関数\(V_\text{out}/V_\text{in}^{+}\)は、負帰還の帰還率\(\beta=V_\text{in}^{-}/V_\text{out}\)と開ループゲイン\(A\)の条件\(A\gg 1\)を利用して
\begin{align}
\frac{V_\text{out}}{V_\text{in}^{+}}=\frac{1}{\frac{1}{A}+\beta}\simeq\frac{1}{\beta} \label{伝達関数}\tag{2}
\end{align}
となる。

ボルテージフォロワ
オペアンプを用いた最もシンプルな負帰還回路がボルテージ・フォロワである。
これは出力電圧を直に反転入力端子に帰還させる回路である(図4参照)。

この場合、単純に\(V_\text{in}^{-}=V_\text{out}\)、すなわち\(\beta=1\)となる。
よって、伝達関数は(\ref{伝達関数})より
\begin{align}
\frac{V_\text{out}}{V_\text{in}^{+}}=1 \label{ボル伝達}\tag{3}
\end{align}
となり、非反転入力端子への入力電圧がそのまま出力される。
一見意味がないように見えるが、実は2つの意味ですごく気の利いた回路になっている。
1つ目は出力電圧の安定性を確保できる点である。
例えば、オペアンプの出力電圧\(V_\text{out}\)が何らかの原因で低下してしまったとする。
すると\(V_\text{in}^{-}\)も同様に下がるので、(\ref{opamp1})を思い出すと、(V_\text{out})が上昇に転じることがわかる。
すなわち、低下してしまった出力電圧を回路自体が元の出力電圧に戻すように制御するのである(図5参照)。
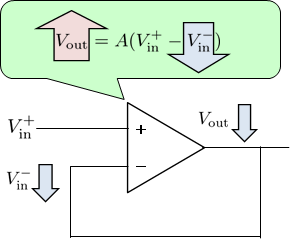
これは逆のパターン、すなわち出力電圧が何らかの原因で上昇しても、同様の流れで出力電圧が下がるように制御される。
2つ目は同電圧で電流増加ができる点である。
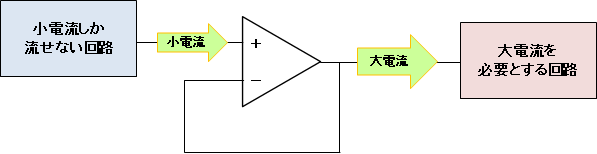
先述した「高入力インピーダンス」かつ「低出力インピーダンス」を思い出すと、ボルテージ・フォロワでは入力電圧と出力電圧が同値だが、出力側からは大きい電流を供給できることがわかる(図6参照)。
この特性は、駆動電流が異なる2つの回路を接続したい場合に有用である。
非反転増幅回路
次に図5のように、信号を反転端子に戻す前に抵抗に通す回路を考える。
これを非反転増幅回路と呼ぶ。
「非反転」と名の付く通り、この回路では\(V_{\text{in}}^{+}\)の位相が反転せずに(要は同位相で)増幅されて\(V_{\text{out}}\)として出力される。
伝達関数(増幅率)は2つの抵抗値の比に依存し、
\begin{align}
\frac{V_{\text{out}}}{V_{\text{in}}^{+}}=1+\frac{R_{1}}{R_{2}} \label{非反転伝達}\tag{4}
\end{align}
となる。

例えば2つの抵抗値が同値であれば2倍に、\(R_{1}\)が\(R_{2}\)の3倍であれば4倍に増幅される。
問題1
非反転増幅回路の伝達関数(\ref{非反転伝達})を導出せよ。
ただし、オペアンプの入力インピーダンスは無限大としてよい。
解答
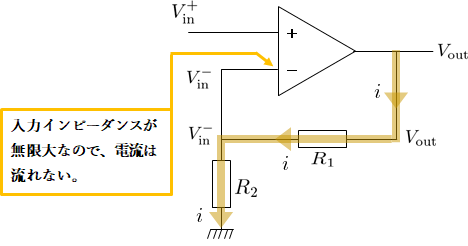
オペアンプの出力端子から抵抗\(R_{1}\)に流れる電流を\(i\)とする。
オペアンプの入力インピーダンスが無限大であるため、オペアンプの入力端子には電流は流れない(図6参照)。
よって電流\(i\)は全て抵抗\(R_{2}\)に流れる。
以上より、オームの法則から
\begin{align}
&V_{\text{out}}-V_{\text{in}}^{-}=iR_{1} \label{非反転オーム1}\tag{5}\\
&V_{\text{in}}^{-}=iR_{2} \label{非反転オーム2}\tag{6}
\end{align}
が成り立つ。
(\ref{非反転オーム2})を(\ref{非反転オーム1})に代入して整理すると、
\begin{align}
V_{\text{out}}-V_{\text{in}}^{-}=\frac{V_{\text{in}}^{-}}{R_{2}}R_{1}\quad \therefore\frac{V_{\text{in}}^{-}}{V_{\text{out}}}=\frac{R_{2}}{R_{1}+R_{2}}\label{非反転beta}\tag{7}
\end{align}
となる。
\(V_{\text{in}}^{-}/V_{\text{out}}=\beta\)であるため、(\ref{非反転beta})を(\ref{伝達関数})に代入すると
\begin{align}
\frac{V_\text{out}}{V_\text{in}^{+}}=\frac{1}{\beta}=\frac{R_{1}+R_{2}}{R_{2}}=1+\frac{R_{1}}{R_{2}}
\end{align}
となる。
反転増幅回路
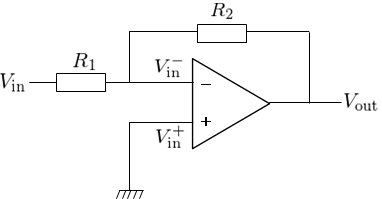
出力と入力が同位相である非反転増幅回路に対し、入力と出力で位相が反転する(逆相になる)回路が反転増幅回路である(図7)。
反転増幅回路も伝達関数は2つの抵抗値の比に依存し、
\begin{align}
\frac{V_{\text{out}}}{V_{\text{in}}}=-\frac{R_{2}}{R_{1}} \label{反転伝達}\tag{8}
\end{align}
となる。
問題2
反転増幅回路の伝達関数(\ref{反転伝達})を導出せよ。
ただし、オペアンプの入力インピーダンスは無限大としてよい。
またオペアンプの開ループゲイン\(A\)について\(1/A\simeq 0\)としてよい。
解答
\(V_{\text{in}}^{+}=0\)より、(\ref{opamp1})から
\begin{align}
V_{\text{out}}=-AV_{\text{in}}^{-} \label{反転1}\tag{9}
\end{align}
となる。
ここで抵抗\(R_{1}\)に流れる電流を\(i\)とする。
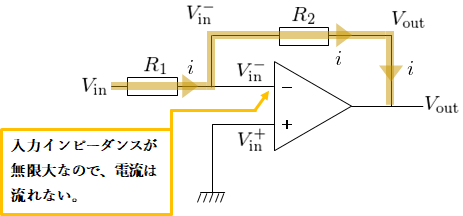
オペアンプの入力インピーダンスが無限大であるため、オペアンプの入力端子には電流は流れない(図8)。
よって電流\(i\)は全て抵抗\(R_{2}\)に流れる。
以上より、オームの法則から
\begin{align}
&V_{\text{in}}-V_{\text{in}}^{-}=iR_{1} \label{反転2}\tag{10}\\
&V_{\text{in}}^{-}-V_{\text{out}}=iR_{2} \label{反転3}\tag{11}
\end{align}
となる。
(\ref{反転2})と(\ref{反転3})より
\begin{align}
\frac{V_{\text{in}}-V_{\text{in}}^{-}}{R_{1}}=\frac{V_{\text{in}}^{-}-V_{\text{out}}}{R_{2}} \label{反転4}\tag{12}
\end{align}
が成り立つため、(\ref{反転4})に(\ref{反転1})を代入して整理すると
\begin{align}
\frac{1}{R_{1}}\left(V_{\text{in}}+\frac{V_{\text{out}}}{A}\right)=\frac{1}{R_{2}}\left(-\frac{V_{\text{out}}}{A}-V_{\text{out}}\right) \quad \therefore\frac{V_{\text{out}}}{V_{\text{in}}}=-\frac{1}{\displaystyle{\frac{1}{A}+\left(1+\frac{1}{A}\right)\frac{R_{1}}{R_{2}}}} \label{反転5}\tag{13}
\end{align}
となる。
ここで\(1/A\simeq 0\)とできるため、(\ref{反転5})は最終的に
\begin{align}
\frac{V_{\text{out}}}{V_{\text{in}}}=-\frac{R_{2}}{R_{1}}
\end{align}
となる。
終わりに
上記3つの回路がオペアンプの基本回路であり、ここから様々な応用回路に派生していく。
次回は、これらの基本回路の応用の1つである演算回路を取り上げようと思う。
次回はこちら。




コメント