【Excelマクロ】移動平均の自動計算とグラフ表示をさせてみた。

Excelマクロ

　会社で不連続データを平滑化して解析を進める必要が生じた。

　データを平滑化する手法としては移動平均を採用したが、平均する項数の最適値を見つける際に、項数を変える度に計算式を書き換えなければならず、かなり面倒だった。

　そこで、平均する項数を入力してボタンを押下するだけで、移動平均を自動で計算し、元データと移動平均後のデータを比較するグラフを同時に描画するマクロを作成した。

Microsoft Excel 2019の利用を想定しています。

広告

サンプル

　今回使うサンプルは下記ボタンから入手可能である。

Excel_Macro_Sample_7.zip ↓

　

　今回のマクロ「exp7_comp.xlsm」を開くと、Sheet1が下図のように表示される。

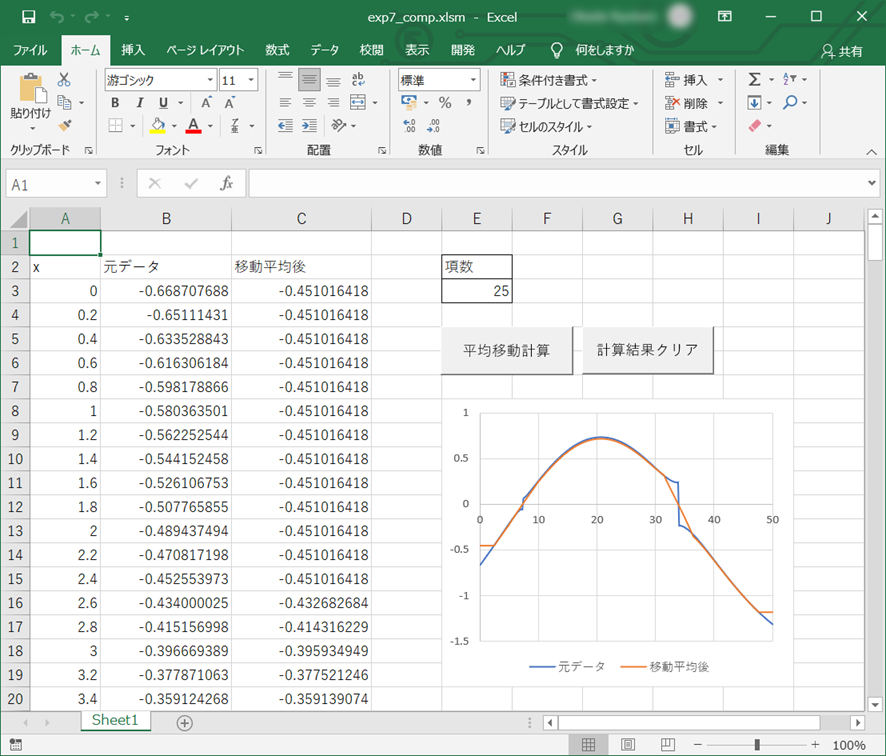
　基本的な使い方は下記のとおりである。

　①　A列に横軸データ、B列に縦軸データを貼り付ける。
　②　E3セルに移動平均の項数を入力する。
　③　「移動平均計算」のボタンを押下する。

　上記手順を実行すると、指定した項数で貼り付けた元データの移動平均を自動で計算し、元データと移動平均後のデータを比較するグラフが描画される。

　項数を変えた結果を見たければ、E3セルの入力値を変えて再度「移動平均計算」ボタンを押下すればよい。

　

　「計算結果クリア」ボタンで、グラフと移動平均計算結果(C列)のデータを消去することができる。

コード詳説

　「exp7_comp.xlsm」には計2つのマクロが保存されている。

移動平均計算およびグラフ作成

　マクロの中身は下記のようになっている。

Sub 移動平均計算およびグラフ作成()

    Dim n As Long
    Dim D As Long
    Dim i As Long
    Dim Graph As Shape
    Dim shp As Shape
    
    
    For Each shp In Worksheets(1).Shapes
        If shp.Type = msoChart Then
            shp.Delete
        End If
    Next


    n = Worksheets(1).Cells(3, 5).Value
    D = Worksheets(1).Cells(3, 1).End(xlDown).Row - 2


    If n Mod 2 = 1 Then

        For i = 0 To D - n
            Worksheets(1).Cells(i + 3 + (n \ 2), 3).Value = _
            WorksheetFunction.Average(Worksheets(1).Range(Cells(i + 3, 2), Cells(i + 3 + 2 * (n \ 2), 2)))
        Next

        For i = 0 To n \ 2
            Worksheets(1).Cells(i + 3, 3).Value = Worksheets(1).Cells(3 + (n \ 2), 3).Value
        Next

        For i = 0 To n \ 2
            Worksheets(1).Cells(i + 3 + (n \ 2) + D - n, 3).Value = _
            Worksheets(1).Cells(D - n + 3 + (n \ 2), 3).Value
        Next

    Else
    
        For i = 0 To D - (n + 1)
            Worksheets(1).Cells(i + 3 + ((n + 1) \ 2), 3).Value = _
            WorksheetFunction.Sum(Worksheets(1).Range(Cells(i + 4, 2), Cells(i + 2 + 2 * ((n + 1) \ 2), 2))) / n _
            + Worksheets(1).Cells(i + 3, 2).Value / 2 / n _
            + Worksheets(1).Cells(i + 3 + 2 * ((n + 1) \ 2), 2).Value / 2 / n
        Next

        For i = 0 To (n + 1) \ 2
            Worksheets(1).Cells(i + 3, 3).Value = Worksheets(1).Cells(3 + ((n + 1) \ 2), 3).Value
        Next

        For i = 0 To (n + 1) \ 2
            Worksheets(1).Cells(i + 3 + ((n + 1) \ 2) + D - (n + 1), 3).Value = _
            Worksheets(1).Cells(D - (n + 1) + 3 + ((n + 1) \ 2), 3).Value
        Next

    End If


    Set Graph = Worksheets(1).Shapes.AddChart2(XlChartType:=xlXYScatterSmoothNoMarkers)
    
    With Graph
        .Top = Worksheets(1).Range("E8:I16").Top
        .Left = Worksheets(1).Range("E8:I16").Left
        .Width = Worksheets(1).Range("E8:I16").Width
    End With

    For i = 2 To 3
        With Graph.Chart
            .SeriesCollection.NewSeries
            .SeriesCollection(i - 1).Name = Worksheets(1).Cells(2, i).Value
            .SeriesCollection(i - 1).XValues = Worksheets(1).Range(Cells(3, 1), Cells(3, 1).End(xlDown))
            .SeriesCollection(i - 1).Values = Worksheets(1).Range(Cells(3, i), Cells(3, i).End(xlDown))
        End With
    Next

    Do While Graph.Chart.SeriesCollection.Count <> 2
        Graph.Chart.FullSeriesCollection(3).Delete
    Loop

    With Graph.Chart
        .HasTitle = False
        .Axes(xlCategory).MinimumScale = _
        WorksheetFunction.Min(Worksheets(1).Range(Cells(3, 1), Cells(3, 1).End(xlDown)))
        .Axes(xlCategory).MaximumScale = _
        WorksheetFunction.Max(Worksheets(1).Range(Cells(3, 1), Cells(3, 1).End(xlDown)))
        .SetElement (msoElementLegendBottom)
    End With

End Sub

　

　まずは

 For Each shp In Worksheets(1).Shapes
    If shp.Type = msoChart Then
        shp.Delete
    End If
 Next

でシート1にあるグラフを一旦全て削除する。

　これは計算をし直す度にグラフが追加されることで、ファイルサイズが大きくなるのを防止するための措置である。

　

　次に変数を定義する。

n = Worksheets(1).Cells(3, 5).Value
D = Worksheets(1).Cells(3, 1).End(xlDown).Row - 2

　nには平均する項数、Dはデータ数をそれぞれ代入する。

　

　次に、メインとなる移動平均の計算に移る。

　計算はIf ～ End If構文で条件分岐している。

　まず、平均する項数が奇数(n mod 2 = 1)の場合は、与えられた項数nからi番目のデータ\(y_{i}\)に対して下記計算を実施し、移動平均値\(y_{i}^{(\text{MA})}\)を求める。

\begin{align}
y_{i}^{(\text{MA})}=\frac{1}{n}\sum_{k=i-\frac{n-1}{2}}^{i+\frac{n-1}{2}}y_{k}
\end{align}

　例えば項数5で、3番目のデータで移動平均を取る場合は

\begin{align}
y_{3}^{(\text{MA})}=\frac{1}{5}\sum_{k=1}^{5}y_{k}=\frac{y_{1}+y_{2}+y_{3}+y_{4}+y_{5}}{5}
\end{align}

となる。

　この計算を実行しているのが下記コードである。

For i = 0 To D - n
    Worksheets(1).Cells(i + 3 + (n \ 2), 3).Value = _
    WorksheetFunction.Average(Worksheets(1).Range(Cells(i + 3, 2), Cells(i + 3 + 2 * (n \ 2), 2)))
Next

　コード中で、平均を計算するAverage関数を利用している。

WorksheetFunction.Average(セル範囲)
⇒　指定したセル範囲中の値での平均値を出力する。

　

　ただし、始めから\(\frac{n-1}{2}\)個分のデータと終わりから\(\frac{n-1}{2}\)個分のデータでは、項数が取れず移動平均の計算ができない。
　(例えば項数5の場合は、データの始めから2個分と終わりの2個分は計算できない。)

　この計算できない部分については、始めから\(\frac{n-1}{2}+1\)番目のデータの移動平均値と最後から\(\frac{n-1}{2}+1\)番目のデータの移動平均値をそのまま代入する。

　この代入処理を実施しているのが下記コードである。

For i = 0 To n \ 2
    Worksheets(1).Cells(i + 3, 3).Value = Worksheets(1).Cells(3 + (n \ 2), 3).Value
Next

For i = 0 To n \ 2
    Worksheets(1).Cells(i + 3 + (n \ 2) + D - n, 3).Value = _
    Worksheets(1).Cells(D - n + 3 + (n \ 2), 3).Value
Next

　前半のFor ～ Next構文では、始めから\(\frac{n-1}{2}\)個分のデータに、始めから\(\frac{n-1}{2}+1\)番目のデータの移動平均値を代入している。

　後半のFor ～ Next構文では、最後から\(\frac{n-1}{2}\)個分のデータに、最後から\(\frac{n-1}{2}+1\)番目のデータの移動平均値を代入している。

　

　続いて、平均する項数が偶数(n mod 2 = 0)の場合だが、この場合移動平均値\(y_{i}^{(\text{MA})}\)は下記のように計算する。

\begin{align}
y_{i}^{(\text{MA})}=\frac{1}{n}\left(\frac{y_{i-\frac{n}{2}}}{2}+\sum_{k=i-\frac{n-2}{2}}^{i+\frac{n-2}{2}}y_{k}+\frac{y_{i+\frac{n}{2}}}{2}\right)
\end{align}

　例えば項数4で、3番目のデータで移動平均を取る場合は

\begin{align}
y_{3}^{(\text{MA})}=\frac{1}{4}\left(\frac{y_{1}}{2}+\sum_{k=2}^{4}y_{k}+\frac{y_{5}}{2}\right)=\frac{1}{4}\left(\frac{y_{1}}{2}+y_{2}+y_{3}+y_{4}+\frac{y_{5}}{2}\right)
\end{align}

となる。

　この計算を実行しているのが下記コードである、

For i = 0 To D - (n + 1)
    Worksheets(1).Cells(i + 3 + ((n + 1) \ 2), 3).Value = _
    WorksheetFunction.Sum(Worksheets(1).Range(Cells(i + 4, 2), Cells(i + 2 + 2 * ((n + 1) \ 2), 2))) / n _
    + Worksheets(1).Cells(i + 3, 2).Value / 2 / n _
    + Worksheets(1).Cells(i + 3 + 2 * ((n + 1) \ 2), 2).Value / 2 / n
Next

　コード中で、総和を計算するSum関数を利用している。

WorksheetFunction.Sum(セル範囲)
⇒　指定したセル範囲中の値の総和を出力する。

　

　また項数が奇数の場合と同様に、項数が偶数の場合も項数が取れず移動平均が計算できない部分が存在する。

　項数が偶数の場合は、始めから\(\frac{n}{2}\)個分のデータと終わりから\(\frac{n}{2}\)個分のデータでは、項数が取れず移動平均の計算ができない。
　(例えば項数4の場合は、データの始めから2個分と終わりの2個分は計算できない。)

　この計算できない部分については、始めから\(\frac{n}{2}+1\)番目のデータの移動平均値と最後から\(\frac{n}{2}+1\)番目のデータの移動平均値をそのまま代入する。

　この代入処理を実施しているのが下記コードである。

For i = 0 To (n + 1) \ 2
    Worksheets(1).Cells(i + 3, 3).Value = Worksheets(1).Cells(3 + ((n + 1) \ 2), 3).Value
Next

For i = 0 To (n + 1) \ 2
    Worksheets(1).Cells(i + 3 + ((n + 1) \ 2) + D - (n + 1), 3).Value = _
    Worksheets(1).Cells(D - (n + 1) + 3 + ((n + 1) \ 2), 3).Value
Next

　前半のFor ～ Next構文では、始めから\(\frac{n}{2}\)個分のデータに、始めから\(\frac{n}{2}+1\)番目のデータの移動平均値を代入している。

　後半のFor ～ Next構文では、最後から\(\frac{n}{2}\)個分のデータに、最後から\(\frac{n}{2}+1\)番目のデータの移動平均値を代入している。

　移動平均の計算は以上である。

　

　後半部分はグラフの描画コードであり、ほとんどは下記記事の解説で事足りるので、詳細な解説は省略することにする。

【Excelマクロ】取り込んだデータからグラフを描画
以前、複数のデータファイルを1つのExcelファイルに集約させるマクロや、 　必要なデータのみを抽出し、1つのシートにまとめて表示させるマクロ を作ってきた。 　今回は時系列データなどを取り込んで、グラフを描画するマクロを作ったので紹介する...
pictblog.com
2021.02.25

　今回新たに登場したコードに、最大値、最小値を出力するコードがあるため、この2つに関しては明示しておく。

WorksheetFunction.Max(セル範囲)
⇒　指定したセル範囲中の値での最大値を出力する。

WorksheetFunction.Min(セル範囲)
⇒　指定したセル範囲中の値での最小値を出力する。

計算結果およびグラフ削除

　マクロの中身は下記のようになっている。

Sub 計算結果およびグラフ削除()

    Dim shp As Shape
    
    For Each shp In Worksheets(1).Shapes
        If shp.Type = msoChart Then
            shp.Delete
        End If
    Next
    
    Range(Range("C3"), Range("C3").End(xlDown)).Select
    Selection.ClearContents
    Worksheets(1).Range("A1").Select
    
End Sub

　前半部分でグラフを削除し、後半部分で移動平均計算結果をクリアしている。

広告

終わりに

　マクロを勉強し始めて半年が経ったが、「この作業、マクロで時短できんじゃね？」と思ってささっと試しに書いたコードがそれなりの働きをすることが増えたように思う。

　だがやはり、まだちょっとでもブランクが空くと構文を忘れるので構文一覧は手放せない。

　どれか1つでいいから、空でコードを記述できる言語を持ちたい…
　(理想はPythonだが。)

　

　END

広告

コメント

タイトルとURLをコピーしました