【AI】機械学習 by Python：分類編⑤～分類モデルの評価～

　前回

の続き。

　今回は分類モデルを評価する指標、その指標を計算するコードを見ていく。

　

実装例

# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.colors import ListedColormap
import sklearn
from sklearn.linear_model import LogisticRegression
from sklearn import metrics

# データセットのインポート
file=pd.read_csv('logistic.csv',header=None)

# データの割り振り
X=file.iloc[:,0:2]
Y=file.iloc[:,2]

# データセットを学習データ（8割）とテストデータ（2割）に分割（random_stateは0）
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)
# 分割の確認
print('分割の確認：',X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)

# 学習実行
# インスタンスの作成
model=LogisticRegression()
# モデルの作成
model.fit(X_train,Y_train)

# 直線の確認
# 切片
print('切片の値 = ', model.intercept_)
# 係数
print('係数の値 = ', model.coef_)

# 学習データからの予測値
pred_train = model.predict(X_train)
# テストデータからの予測値
pred_test = model.predict(X_test)

# 学習データを用いた分類モデルの評価
print('正解率(学習データ) = ', metrics.accuracy_score(Y_train, pred_train))
print('適合率(学習データ) = ', metrics.precision_score(Y_train, pred_train))
print('再現率(学習データ) = ', metrics.recall_score(Y_train, pred_train))
print('F値(学習データ) = ', metrics.f1_score(Y_train, pred_train))

# テストデータを用いた分類モデルの評価
print('正解率(テストデータ) = ', metrics.accuracy_score(Y_test, pred_test))
print('適合率(テストデータ) = ', metrics.precision_score(Y_test, pred_test))
print('再現率(テストデータ) = ', metrics.recall_score(Y_test, pred_test))
print('F値(テストデータ) = ', metrics.f1_score(Y_test, pred_test))

# データセットおよび直線の図示
plt.figure(figsize=(4,4))
plt.scatter(file.iloc[:,0], file.iloc[:,1],c=file.iloc[:,2], cmap=ListedColormap(['#FF0000', '#0000FF']))
plt.plot(file.iloc[:,0], -file.iloc[:,0]*model.coef_[0,0]/model.coef_[0,1]-model.intercept_[0]/model.coef_[0,1])
plt.show()

出力例

分割の確認： (160, 2) (40, 2) (160,) (40,)
切片の値 =  [-9.71024304]
係数の値 =  [[0.04871103 1.89741032]]
正解率(学習データ) =  0.91875
適合率(学習データ) =  0.9195402298850575
再現率(学習データ) =  0.9302325581395349
F値(学習データ) =  0.9248554913294798
正解率(テストデータ) =  0.875
適合率(テストデータ) =  0.8125
再現率(テストデータ) =  0.8666666666666667
F値(テストデータ) =  0.8387096774193549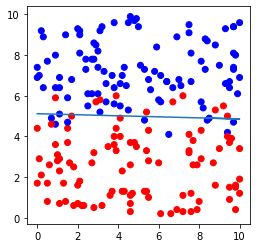

　実際にプログラムを実行したい場合は、下記ボタンよりcsvファイル「logistic.csv」をダウンロードしてプログラムの保存先に保存すること。

8. 分類モデルの評価

　前回に予測値を導入したため、ここで実際に分類モデルの評価に入る。

# 学習データを用いた分類モデルの評価
print('正解率(学習データ) = ', metrics.accuracy_score(Y_train, pred_train))
print('適合率(学習データ) = ', metrics.precision_score(Y_train, pred_train))
print('再現率(学習データ) = ', metrics.recall_score(Y_train, pred_train))
print('F値(学習データ) = ', metrics.f1_score(Y_train, pred_train))

# テストデータを用いた分類モデルの評価
print('正解率(テストデータ) = ', metrics.accuracy_score(Y_test, pred_test))
print('適合率(テストデータ) = ', metrics.precision_score(Y_test, pred_test))
print('再現率(テストデータ) = ', metrics.recall_score(Y_test, pred_test))
print('F値(テストデータ) = ', metrics.f1_score(Y_test, pred_test))

　分類モデルを評価する指標にはいくつか種類があるが、今回は代表的な指標である正解率、適合率、再現率、F値を実際に計算させている。

　

　ここで上にあげた指標の説明のために、100個のデータがあり、90個がカテゴリーAに、10個がカテゴリーBに属している簡単なモデルを考える。

　そして分類学習の結果、本来カテゴリーAに属するはずのデータの内4つがカテゴリーBに、本来カテゴリーBに属するはずのデータの内2つがカテゴリーAに分類され、結果、88個のデータがカテゴリーAに、12個のデータがカテゴリーBに分類されたとする。

	実際のデータ数	分類学習で予測したデータ数
A	90	88 (内2個が本来はカテゴリーB)
B	10	12 (内4個が本来はカテゴリーA)

　

　まずは正解率だが、これは単純に予測したデータ数に対する正解したデータ数の割合である。
　今回の例では、予測したデータ数100に対し、正しくカテゴリーAに分類されているデータは86個、正しくカテゴリーBに分類されているデータは8個であるため、

\begin{align}
正解率=\frac{86+8}{100}=0.94
\end{align}

と求められる。
　単純な指標ゆえに注意が必要で、データ分布に大きな偏りがある場合は正しく評価できない場合が多い。

は正解率を計算するためのコードである。

　

　次に適合率。
　こちらは特定のカテゴリーの予測データ数に対して、正しくそのカテゴリーに分類されたデータ数の割合である。
　カテゴリーAに着目すると、カテゴリーAに分類されたデータ数は88個であり、その内正しくカテゴリーAに分類されたのは86個であるから、

\begin{align}
適合率=\frac{86}{88}=0.977
\end{align}

となる。

は適合率を計算するためのコードである。

　

　続いて再現率。
　適合率と同じく特定のカテゴリーに着目するが、こちらは実際のカテゴリーのデータ数に対して、分類モデルが正しくそのカテゴリーに分類したデータ数の割合である。
　カテゴリーAに着目すると、実際のカテゴリーAのデータ数は90個であり、分類モデルが正しくカテゴリーAに分類したデータ数は86個であるから

\begin{align}
再現率=\frac{86}{90}=0.956
\end{align}

となる。

は再現率を計算するためのコードである。

　

　最後にF値だが、これは適合率と再現率の調和平均であり

\begin{align}
\text{F値}=\frac{2}{\displaystyle{\frac{1}{適合率}+\frac{1}{再現率}}}
\end{align}

で定義される。
　今回の場合では、上の計算結果を利用して

\begin{align}
\text{F値}=\frac{2}{\displaystyle{\frac{1}{0.977}+\frac{1}{0.956}}}=0.966
\end{align}

となる。
　F値は、適合率と再現率がトレードオフの関係にあることを踏まえ、両者を同時に踏まえた評価をするために用いられる。
　適合率と再現率の両者が同等かつ高い値を示すほど、F値は高い値を示す。

はF値を計算するためのコードである。

　

　実装例のコードを詳しく見ていくと次のようになる。

print('正解率(学習データ) = ', metrics.accuracy_score(Y_train, pred_train))

⇒学習データとその予測値を使って正解率を算出し、print関数で出力するコード。
　出力例としては下記にようになる。

正解率(学習データ) =  0.91875

　

print('適合率(学習データ) = ', metrics.precision_score(Y_train, pred_train))

⇒学習データとその予測値を使って適合率を算出し、print関数で出力するコード。
　出力例としては下記にようになる。

適合率(学習データ) =  0.9195402298850575

　

print('再現率(学習データ) = ', metrics.recall_score(Y_train, pred_train))

⇒学習データとその予測値を使って再現率を算出し、print関数で出力するコード。
　出力例としては下記にようになる。

再現率(学習データ) =  0.9302325581395349

　

print('F値(学習データ) = ', metrics.f1_score(Y_train, pred_train))

⇒学習データとその予測値を使ってF値を算出し、print関数で出力するコード。
　出力例としては下記にようになる。

F値(学習データ) =  0.9248554913294798

　

　続くコードはテストデータとその予測値から正解率、適合率、再現率、F値を計算して表示するコードであり、基本は上記の説明と変わらないので省略する。

次回予告

　次回が分類学習の実装例解説のラスト。

　最後に分類結果をグラフで可視化するコードを見ていく。

　

　END

　

　※追記
　結果をグラフにして可視化するコードについて。