前回
にて、外力がかからない2物体間の衝突を見てきた。
今回は重力がかかった質点が動かない物体(床、壁)に衝突した際の振る舞いを扱っていく。
ただし、今回は動かない物体の表面はなめらかであり、摩擦は起きない場合を想定する。
考え方
重力がかかった質点となめらかな床や壁の衝突は、反発係数の式と投射運動の式の連立方程式で記述できる。
反発係数の式
\begin{gather}
e=-\frac{v’}{v} \label{反発}\tag{1}
\end{gather}
(\(e\):反発係数、\(v\):衝突前の速度、\(v’\):衝突後の速度)
+
投射運動の式
\begin{gather}
v=v_{0}+at \label{投射1}\tag{2}\\
x=x_{0}+v_{0}t+\frac{1}{2}at^{2} \label{投射2}\tag{3}\\
v^{2}-v_{0}^{2}=2a(x-x_{0})\label{投射3}\tag{4}\\
\end{gather}
(\(t\):時間、\(a\):加速度、\(v\):速度、\(v_{0}\):初速度、\(x\):変位、\(x_{0}\):初期位置)
これらを具体的にどのように利用するかは、後述の問題演習で詳しく見ていく。
問題1
問題1
高さ\(h[\text{m}]\)の台上の端から小球を水平右向きに水平投射する。やがて小球はなめらかな床に衝突して跳ね返った。
重力加速度を\(g[\text{m/s}^{2}]\)、水平投射の初速度を\(v_{0}[\text{m/s}]\)、小球と床の間の鉛直方向の反発係数を\(0<e<1\)とする。
また小球は十分小さく、空気抵抗は無視できるとする。
(1) 1回目の床との衝突直後の小球の速さを求めよ。

(2) \(n\)回目の床との衝突直後の小球の速さを求めよ。
(3) 十分に時間が経過した後の小球の運動を記述せよ。
解説
水平右向き、鉛直上向きを正にとる。また、床面を鉛直方向の基準にとる。
(1)
床はなめらかであるため、衝突前後で水平方向の速度は変化しない。
よって鉛直方向の速度のみ求めればよい。
衝突前の小球の速度を\(v[\text{m/s}]\)、衝突前の鉛直方向の速度を\(v_{y}[\text{m/s}]\)、衝突後の小球の速度を\(v'[\text{m/s}]\)、衝突後の鉛直方向の速度を\(v’_{y}[\text{m/s}]\)とする。
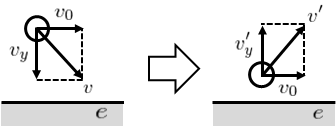
このとき、衝突前の小球の鉛直方向の速度\(v_{y}\)は投射運動の式(\ref{投射3})より
\begin{gather}
v_{y}^{2}-0^{2}=2(-g)(0-h)\\
v_{y}^{2}=2gh
\therefore v_{y}=-\sqrt{2gh}\quad(v_{y}<0より)\label{1-1}\tag{5}
\end{gather}
となるため、衝突後の小球の鉛直方向の速度\(v’_{y}\)は反発係数の式(\ref{反発})と(\ref{1-1})より
\begin{gather}
e=-\frac{v’_{y}}{v_{y}}=-\frac{v’_{y}}{-\sqrt{2gh}}\\
\therefore v’_{y}=e\sqrt{2gh} \label{1-2}\tag{6}
\end{gather}
となる。
よって求める速さ\(|v’|\)は
\begin{gather}
|v’|=\sqrt{v_{0}^{2}+{v’_{y}}^{2}}=\sqrt{v_{0}^{2}+2e^{2}gh}\quad\therefore \boxed{|v’|=\sqrt{v_{0}^{2}+2e^{2}gh}}
\end{gather}
となる。
(2)
鉛直方向のみの運動に着目する。
鉛直方向の速度\(v_{\text{up}}=|v_{\text{up}}|\)で床を跳ね返った小球は、再び床に衝突する直前には同じ速さの速度\(v_{\text{down}}=-|v_{\text{up}}|\)に達する。
そして床に衝突した直後は、鉛直方向の速さは\(e\)倍になる。
上記の速度変化を繰り返すため、衝突の度に鉛直方向の速さは\(e\)倍される。
よって、1回目の衝突直後の鉛直方向の速さは\(e\sqrt{2gh}\)であるため、\(n\)回目の衝突直後の鉛直方向の速さは\(e^{n}\sqrt{2gh}\)となる。
以上より、求める速さを\(|v’_{n}|\)とすると\(\boxed{|v’_{n}|=\sqrt{v_{0}^{2}+2e^{2n}gh}}\)となる。
この答えが正しいかどうか確かめるには、数学的帰納法を使えばよい。
(i) \(n=1\)のとき
\(|v’_{1}|=\sqrt{v_{0}^{2}+2e^{2}gh}\)となり、(1)の答えと一致する。
(ii) \(n=k\)のとき
\(|v’_{k}|=\sqrt{v_{0}^{2}+2e^{2k}gh}\)が成立すると仮定する。
(iii) \(n=k+1\)のとき
\(k+1\)回目の衝突前の鉛直方向の速度は、\(k\)回目の衝突後の鉛直方向の速度とちょうど逆向きである。
よって\(n\)回目の衝突後の鉛直方向の速度を\(v’_{n,y}\)とすると、\(k+1\)回目の衝突後の鉛直方向の速度\(v’_{k+1,y}\)は反発係数の式(\ref{反発})より
\begin{gather}
e=-\frac{v’_{k+1,y}}{-v’_{k,y}}=\frac{v’_{k+1,y}}{e^{k}\sqrt{2gh}}\quad \therefore v’_{k+1,y}=e^{k+1}\sqrt{2gh}
\end{gather}
となる。
よって\(k+1\)回目の衝突後の速さは
\begin{gather}
|v’_{k+1}|=\sqrt{v_{0}^{2}+{v’_{k+1,y}}^{2}}=\sqrt{v_{0}^{2}+2e^{2(k+1)}gh}
\end{gather}
となり、(ii)の仮定と辻褄が合う。
(3)
(2)で求めた\(|v’_{n}|\)において\(n\)を無限にとばせば良い。
\(e<1\)より\(n\to\infty\)のとき\(e^{n}\to 0\)となる。
よってこのとき、\(|v’_{n\to\infty}|=\sqrt{v_{0}^{2}}=v_{0}\)となり、鉛直方向の成分がなくなる。
よって十分時間が経過すると、小球は床面を水平右向きに速さ\(v_{0}\)で等速運動するようになる。
問題2
問題2
鉛直でなめらかな壁をもつ高さ\(4.9\,\text{m}\)の2つの台が\(4\,\text{m}\)の間隔を空けて並んでいる。
そのうちの1つの台の上端から、小球を水平右向きに初速度\(v_{0}\)で打ち出す。
2つの台の中間地点となる床には箱が置かれており、この箱に小球を投げ入れたい。
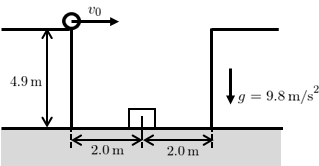
小球の壁への衝突が2回以内であるとき、小球が箱に入るための初速度\(v_{0}\)を全て求めよ。
ただし、重力加速度は\(g=9.8\,\text{m/s}^{2}\)、小球と2つの壁との間の反発係数はいずれも\(e=1/2\)であり、空気抵抗は無視できるとする。
解説
水平右向き、鉛直下向きを正にとり、小球の初期位置を原点とする。
小球が箱に入るパターンは、(i)壁に衝突せずに箱に入る、(ii)右側の壁に1回だけ衝突して箱に入る、(iii)両側の壁に1回ずつ衝突して箱に入る、の3種類である。
それぞれのパターンについて考える。
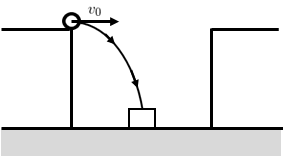
(i) 壁に衝突しない場合
台上からの水平投射後に、小球が直接箱に入ればよい。
台上から小球が水平投射で床に到達するまでの時間を\(t\)とすると、時間\(t\)後の小球の鉛直方向の変位を\(y\)、小球の鉛直方向の初期位置を\(y_{0}\)、小球の鉛直方向の初速度を\(v_{0y}\)としてとして(\ref{投射2})より
\begin{gather}
y=y_{0}+v_{0y}t+\frac{1}{2}gt^{2}\\
4.9\,\text{m}=0\,\text{m}+0\,\text{m/s}\times t+\frac{1}{2}\times 9.8\,\text{m/s}^{2}\times t^{2}\\
t^{2}=1.0\,\text{s}^{2}\quad\therefore t=1.0\,\text{s}\label{2-3}\tag{7}
\end{gather}
となる。
よって\(t=1.0\,\text{s}\)までに小球が水平右向きに\(2.0\,\text{m}\)進んでいれば、小球は直接箱に入ることがわかる。
以上より、\(t=1.0\,\text{s}\)後の小球の水平方向の変位を\(x\)とすると、求める初速度は
\begin{gather}
x=v_{0}t\\
2.0\,\text{m}=v_{0}\times 1.0\,\text{s}\quad \therefore \boxed{v_{0}=2.0\,\text{m/s}}
\end{gather}
となる。
(ii) 壁に1回衝突する場合
右側の壁に1度衝突した後に箱に入る場合を考える。
右側の壁に衝突した直後の小球の水平方向の速度を\(v_{x}\)とすると、反発係数の式(\ref{反発})より
\begin{gather}
e=-\frac{v_{x}}{v_{0}}\\
\frac{1}{2}=-\frac{v_{x}}{v_{0}}\quad\therefore v_{x}=-\frac{v_{0}}{2}\label{2-1}\tag{8}
\end{gather}
となる。
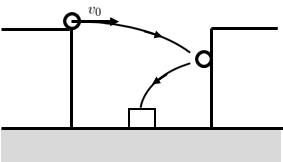
よって、小球が投射開始から右側の壁に衝突するまでの時間を\(t_{1}\)、小球が右側の壁から跳ね返ってから箱に入るまでの時間を\(t_{2}\)とすると、小球が投射開始から箱に入るまでの時間\(t\)は
\begin{gather}
t=t_{1}+t_{2}=\frac{4.0\,\text{m}}{v_{0}}+\frac{2.0\,\text{m}}{|v_{x}|}=\frac{4.0\,\text{m}}{v_{0}}+\frac{2.0\,\text{m}}{v_{0}/2}=\frac{8.0\,\text{m}}{v_{0}}\\
\therefore t=\frac{8.0\,\text{m}}{v_{0}}\label{2-2}\tag{9}
\end{gather}
となる。
一方、鉛直方向の運動は(i)と同じであるため、小球が水平投射後から床に到達するまでの時間は(\ref{2-3})より\(t=1.0\,\text{s}\)となる。
よって(\ref{2-3})と(\ref{2-2})が一致すればよいため、
\begin{gather}
1.0\,\text{s}=\frac{8.0\,\text{m}}{v_{0}}\quad\therefore \boxed{v_{0}=8.0\,\text{m/s}}
\end{gather}
となる。
(iii) 壁に2回衝突する場合
両方の壁に1回ずつ衝突する場合を考える。
左側の壁に衝突した直後の小球の水平方向の速度を\(v’_{x}\)とすると、反発係数の式(\ref{反発})と(\ref{2-1})より
\begin{gather}
e=-\frac{v’_{x}}{v_{x}}\\
\frac{1}{2}=-\frac{v_{x}}{-v_{0}/2}\quad\therefore v’_{x}=\frac{v_{0}}{4}\label{2-4}\tag{10}
\end{gather}
となる。
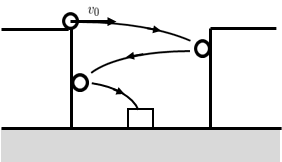
よって、小球が投射開始から右側の壁に衝突するまでの時間を\(t’_{1}\)、小球が右側の壁から跳ね返ってから左側の壁に衝突するまでの時間を\(t’_{2}\)、小球が左側の壁から跳ね返ってから箱に入るまでの時間を\(t’_{3}\)とすると、小球が投射開始から箱に入るまでの時間\(t\)は
\begin{align}
t&=t’_{1}+t’_{2}+t’_{3}\\
&=\frac{4.0\,\text{m}}{v_{0}}+\frac{4.0\,\text{m}}{|v_{x}|}+\frac{2.0\,\text{m}}{v’_{x}}\\
&=\frac{4.0\,\text{m}}{v_{0}}+\frac{4.0\,\text{m}}{v_{0}/2}+\frac{2.0\,\text{m}}{v_{0}/4}=\frac{20\,\text{m/s}}{v_{0}}\quad\therefore t=\frac{20\,\text{m/s}}{v_{0}}\label{2-5}\tag{11}
\end{align}
となる。
一方、鉛直方向の運動は(ii)と同様に(i)と同じであるため、小球が水平投射後から床に到達するまでの時間は(\ref{2-3})より\(t=1.0\,\text{s}\)となる。
よって(\ref{2-3})と(\ref{2-5})が一致すればよいため、
\begin{gather}
1.0\,\text{s}=\frac{20\,\text{m}}{v_{0}}\quad\therefore \boxed{v_{0}=20\,\text{m/s}}
\end{gather}
となる。
終わりに
今回はそこそこ難易度が高い問題を扱ったが、逆にこれらが楽に解ければ相応の実力が身についているだろう。
次はまた別の力学のテーマで記事を書きたいが、何にしようか…
END





コメント