高校物理最初の大きな関門である、投射運動の考え方について解説する。
まずは水平投射から。
考え方
結論から言うと、水平投射は等速直線運動と自由落下の組み合わせである。
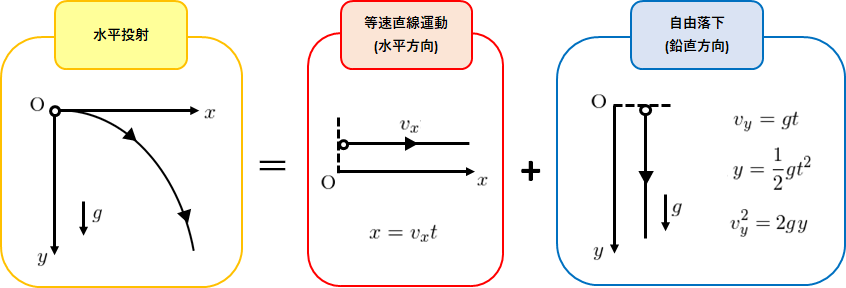
水平方向と鉛直方向で別々に運動を考えて立式し、連立方程式の問題として考えれば大概の問題は解ける。
例題
上記の考え方を念頭に入れた上で、水平投射の例題を解いてみる。
例題
崖の上にある質点を、水平右向きに初速度を与えて落下させる。水平方向の初速度が\(2.0\,\text{m/s}\)であり、落下し始めた時間を\(0\,\text{s}\)とするとき、次の問いに答えよ。
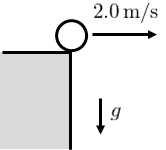
(1) 質点が落下開始から\(4.9\,\text{m}\)落下したときの、質点の水平方向の速さ\(|v_{x}|\)、鉛直方向の速さ\(|v_{y}|\)を求めよ。
(2) 質点が落下開始から\(19.6\,\text{m}\)落下した時点で、質点が水平方向に進んだ距離\(x\)を求めよ。
ただし空気抵抗は無視してよく、重力加速度を\(g=9.8\,\text{m/s}^{2}\)とする。
解説
質点の運動は水平投射であり、水平方向は等速直線運動、鉛直方向は自由落下である。
水平右向き、および鉛直下向きを正にとる。
(1)
水平方向は等速直線運動であるため、時間に依らず速度は一定である。
よって水平方向の速さは初速度そのままであり\(\boxed{|v_{x}|=2.0\,\text{m/s}}\)となる。
鉛直方向の速さは自由落下の式より
\begin{align}
v_{y}^{2}=2gy=2\cdot 9.8\,\text{m/s}^{2}\cdot 4.9\,\text{m}=4\cdot4.9^{2}\,\text{m/s}\quad\therefore v_{y}=9.8\,\text{m/s}
\end{align}
となるため\(\boxed{|v_{y}|=9.8\,\text{m/s}}\)となる。
(2)
水平方向の運動は等速直線運動であり、速度は与えられた初速度\(v_{0x}=2.0\,\text{m/s}\)で一定であるため、運動した時間\(t\)がわかればよい。
質点は落下開始から\(19.6\,\text{m}\)落下しているため、自由落下の式から
\begin{align}
&y=\frac{1}{2}gt^{2} \\
&19.6\,\text{m}=\frac{1}{2}\cdot 9.8\,\text{m/s}^{2}\cdot t^{2}\quad \therefore t=2.0\,\text{s}
\end{align}
となり、運動した時間を求められる。
よってこの時間を利用すれば、水平方向に進んだ距離\(x\)は
\begin{align}
x=v_{0x}t=2.0\,\text{m/s}\cdot 2.0\,\text{s}=4.0\,\text{m}\quad \therefore\boxed{x=4.0\,\text{m}}
\end{align}
となる。
終わりに
水平投射と来たら次は斜方投射である。
斜方投射も水平投射と同じ考え方で問題を解くことができる。
斜方投射については下記記事を参照。





コメント