【フーリエ解析】フーリエ級数～問題演習～

　大学時代のノートを見返していたところ、フーリエ級数の応用問題を見つけたので解き直してみた。

問題

　以下の各問に答えよ。ただし全問題において$m,n$は正の整数とする。

(1)　$\displaystyle{\int_{-\pi}^{\pi}\cos(nx)dx,\,\int_{-\pi}^{\pi}\cos(mx)\cos(nx)dx}$を計算せよ。

(2)　$\displaystyle{f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_{n}\cos(nx)}$のとき、$\displaystyle{\int_{-\pi}^{\pi}f(x)dx,\,\int_{-\pi}^{\pi}f(x)\cos(nx)dx}$を計算せよ。

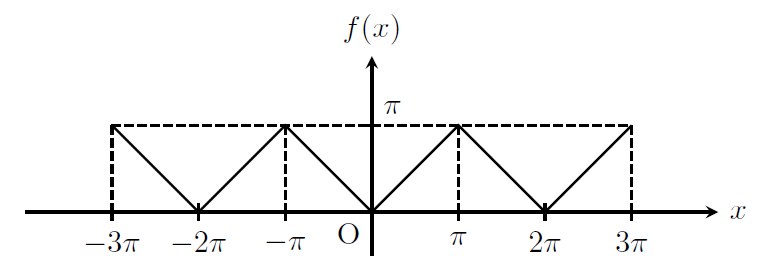
(3)　$f(x)$が以下の周期関数のとき、(2)における$a_0$および$a_{n}\,(n\ge1)$を求めよ。

$$\begin{align} f(x)=|x|\, (-\pi<x\leq \pi),\quad f(x+2\pi)=f(x) \end{align}$$

(4)　(3)の結果を用いて、無限級数$\displaystyle{\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\cdots=\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2}}$の値を求めよ。

解説

(1)

　実際に計算する。

$$\begin{align} &\int_{-\pi}^{\pi}\cos(nx)dx=\left[\frac{1}{n}\sin(nx)\right]_{-\pi}^{\pi}=\boxed{0}\\ \\ &\int_{-\pi}^{\pi}\cos(mx)\cos(nx)dx\\ =&\int_{-\pi}^{\pi}\frac{\cos(m+n)x+\cos(m-n)x}{2}dx \qquad \text{(和積の公式より)} \\ =&\begin{cases} \displaystyle{\frac{1}{2}\int_{-\pi}^{\pi}\left\{\cos(2mx)+1\right\}dx} &(m=n) \\ \displaystyle{\frac{1}{2}\int_{-\pi}^{\pi}\{\cos(m+n)x+\cos(m-n)x\}dx} &(m\neq n) \\ \end{cases} \\ =&\begin{cases} \displaystyle{\frac{1}{2}\left[\frac{1}{2m}\sin(2mx)+x\right]_{-\pi}^{\pi}} &(m=n) \\ \displaystyle{\frac{1}{2}\left[\frac{1}{m+n}\sin(m+n)x+\frac{1}{m-n}\sin(m-n)x\right]_{-\pi}^{\pi}} &(m\neq n) \\ \end{cases} \\ =&\boxed{\begin{cases} \displaystyle{\pi} &(m=n) \\ \displaystyle{0} &(m\neq n) \\ \end{cases}} \end{align}$$

　

(2)

　実際に計算する。

$$\begin{align} \int_{-\pi}^{\pi}f(x)dx&=\int_{-\pi}^{\pi}\left\{\frac{a_0}{2}+\sum_{n=1}^{\infty}a_{n}\cos(nx)\right\}dx \\ &=\int_{-\pi}^{\pi}\frac{a_{0}}{2}dx+\sum_{n=1}^{\infty}\int_{-\pi}^{\pi}a_{n}\cos(nx)dx \\ &=\frac{a_{0}}{2}\int_{-\pi}^{\pi}dx+\sum_{n=1}^{\infty}a_{n}\int_{-\pi}^{\pi}\cos(nx)dx \\ &=\frac{a_{0}}{2}\cdot{2}\pi \qquad \text{((1)の結果より第2項の積分が0になる。)}\\ &=\boxed{\pi{a_{0}}}\label{for.3.3.1}\tag{1} \end{align}$$

$$\begin{align} \int_{-\pi}^{\pi}f(x)\cos(nx)dx&=\int_{-\pi}^{\pi}\left\{\frac{a_0}{2}+\sum_{k=1}^{\infty}a_{k}\cos(kx)\right\}\cos(nx)dx \\ &=\int_{-\pi}^{\pi}\frac{a_0}{2}\cos(nx)dx+\sum_{k=1}^{\infty}\int_{-\pi}^{\pi}a_{k}\cos(kx)\cos(nx)dx \\ &=\frac{a_0}{2}\int_{-\pi}^{\pi}\cos(nx)dx+\sum_{k=1}^{\infty}a_{k}\int_{-\pi}^{\pi}\cos(kx)\cos(nx)dx \\ &=0+\sum_{k=1}^{\infty}a_{k}\int_{-\pi}^{\pi}\cos(kx)\cos(nx)dx \qquad \text{((1)の結果より)} \\ &=a_{n}\int_{-\pi}^{\pi}\cos(nx)\cos(nx)dx \qquad \text{((1)の結果より)} \\ &=\boxed{\pi{a_{n}}} \qquad \text{((1)の結果より)} \label{for.3.3.3}\tag{2} \end{align}$$

　

(3)

　まず$a_{0}$について。式($\ref{for.3.3.1}$)を変形して計算を進めれば、

$$\begin{align} a_{0}&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx \\ &=\frac{1}{\pi}\left\{\int_{-\pi}^{0}(-x)\,dx+\int_{0}^{\pi}x\,dx\right\} \\ &=\frac{1}{\pi}\left\{\left[-\frac{1}{2}x^{2}\right]_{-\pi}^{0}+\left[\frac{1}{2}x^{2}\right]_{0}^{\pi}\right\}=\frac{1}{\pi}\left(\frac{\pi^{2}}{2}+\frac{\pi^{2}}{2}\right)=\pi \label{for.3.3.2}\tag{3} \end{align}$$

となる。
　続いて$a_{n}\,(n\ge1)$について。式($\ref{for.3.3.3}$)を変形して計算を進めれば、

$$\begin{align} a_{n}&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx \\ &=\frac{1}{\pi}\left\{\int_{-\pi}^{0}(-x\cos(nx))dx+\int_{0}^{\pi}x\cos(nx)dx\right\} \\ &=\frac{1}{\pi}\left\{\int_{0}^{-\pi}x\cos(nx)dx+\int_{0}^{\pi}x\cos(nx)dx\right\} \\ &=\frac{1}{\pi}\left\{\left[\frac{x}{n}\sin(nx)\right]_{0}^{-\pi}-\int_{0}^{-\pi}\frac{1}{n}\sin(nx)dx+\left[\frac{x}{n}\sin(nx)\right]_{0}^{\pi}-\int_{0}^{\pi}\frac{1}{n}\sin(nx)dx\right\} \\ &=\frac{1}{\pi}\left\{\frac{1}{n}\int_{-\pi}^{0}\sin(nx)dx-\frac{1}{n}\int_{0}^{\pi}\sin(nx)dx\right\} \\ &=\frac{1}{\pi}\left\{\frac{1}{n}\left[-\frac{1}{n}\cos(nx)\right]_{-\pi}^{0}-\frac{1}{n}\left[-\frac{1}{n}\cos(nx)\right]_{0}^{\pi}\right\} \\ &=\frac{1}{{\pi}n^{2}}\{-1+\cos(-n\pi)+\cos(n\pi)-1\} \\ &=\frac{1}{{\pi}n^{2}}\{\cos(n\pi)+\cos(n\pi)-2\} \qquad \text{(一般に$\cos(-x)=\cos{x}$より)}\\ &=\frac{2}{{\pi}n^{2}}\{\cos(n\pi)-1\}=\frac{2}{{\pi}n^{2}}\{(-1)^{n}-1\} \label{for.3.3.4}\tag{4} \end{align}$$

　よって式($\ref{for.3.3.2}$)、式($\ref{for.3.3.4}$)より、

$$\begin{align} \boxed{a_{0}=\pi \qquad a_{n}=\frac{2}{{\pi}n^{2}}\{(-1)^{n}-1\}} \end{align}$$

　

(4)

　(3)の結果を利用すると$f(x)$は、

$$\begin{align} f(x)=\frac{\pi}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n}-1}{n^{2}}\cos(nx) \label{for.3.4.1}\tag{5} \end{align}$$

となる。
　ここで式($\ref{for.3.4.1}$)において$x=\pi$とすると、

$$\begin{align} f(\pi)=&\frac{\pi}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n}-1}{n^{2}}\cos(n\pi) \\ =&\frac{\pi}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{(-1)^{n}-1}{n^{2}}(-1)^{n} \\ =&\frac{\pi}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{1-(-1)^{n}}{n^{2}} \\ =&\frac{\pi}{2}+\frac{2}{\pi}\left(2+\frac{2}{3^{2}}+\frac{2}{5^{2}}+\cdots\right) \\ =&\frac{\pi}{2}+\frac{4}{\pi}\left(\frac{1}{1^{2}}+\frac{1}{3^{2}}+\frac{1}{5^{2}}+\cdots\right) \\ =&\frac{\pi}{2}+\frac{4}{\pi}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \label{for.3.4.2}\tag{6} \end{align}$$

　よってもともと$f(x)=|x|\,(-\pi<x\leq \pi)$であり、$f(\pi)=\pi$であるため、式($\ref{for.3.4.2}$)から、

$$\begin{align} &\pi=\frac{\pi}{2}+\frac{4}{\pi}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \\ &\frac{\pi}{2}=\frac{4}{\pi}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \\ &\frac{\pi^{2}}{8}=\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} &\boxed{\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2}=\frac{\pi^{2}}{8}} \end{align}$$

終わりに

　本来であればフーリエ級数の解説記事から先に書くべきだろうが、それはフーリエ変換と合わせて後で作成することにする。

　仕事でもフーリエ変換を使っているからできればその話もしたい。
　(もちろん内容はある程度ぼかすが。)

　

　END