前回
にてフーリエ解析の手法の1つであるフーリエ級数を見てきた。
本記事では、フーリエ解析のもう1つの手法であるフーリエ変換について扱う。
こちらも詳細な議論は教科書に一任する。
(短めに終わらせたいが長くなるかもしれないことを踏まえて、できない可能性がある約束はしない。)
概要
任意の関数\(f(x)\)に対し、フーリエ変換\(F(\alpha)\)を次式で定義する。
\begin{align}
F(\alpha)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ix\alpha}dx \label{フーリエ変換定義式}\tag{1}
\end{align}
このとき\(f(x)\)を\(F(\alpha)\)を用いて表わすフーリエ逆変換は次式のようになる。
\begin{align}
f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}F(\alpha)e^{ix\alpha}d\alpha \label{フーリエ逆変換定義式}\tag{2}
\end{align}
フーリエ級数では周期関数を対象としていたが、フーリエ変換では非周期関数でも良い。
ここで\(x\)と\(\alpha\)の関係に注目してほしい。
(\ref{フーリエ変換定義式})の指数関数の肩を見ると、虚数単位\(i\)と\(x\)および\(\alpha\)の積となっている。
指数関数の肩は無次元量のはずであるため、\(x\)と\(\alpha\)は互いに逆数の次元をもつことがわかる。
フーリエ変換とは、もとの関数がもつ情報を、逆数の次元をもつ変数の関数で記述する操作なのである。
物理での例として、互いに逆数の次元をもつ物理量に「時間」と「角周波数」がある。
ゆえに時間の関数をフーリエ変換することを、「時間領域から周波数領域へ変換する」と表現することがある。
例題
ここで、実際に時間の関数をフーリエ変換してみる。
例題
次の時間の関数\(f(t)\)のフーリエ変換を求めよ。ただし\(A\neq 0\)は定数、\(\omega_{0}>0\)は角周波数、\(T>0\)は時間の次元をもつ正の定数である。
\begin{align}
f(t)=\begin{cases}A\cos\omega_{0}t &(-T\leq t \leq T) \\0&(t<-T,t>T) \label{矩形時間波形}\tag{3}
\end{cases}
\end{align}
解説
\(f(t)\)のグラフを描くと下図のようになる。
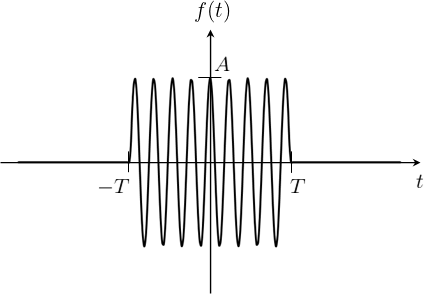
\(-T\leq t\leq T\)の範囲では角周波数\(\omega_{0}\)の周期関数、それ以外は0という関数だ。
実際に角周波数を\(\omega\)として、\(f(t)\)のフーリエ変換を計算する。
\begin{align}
F(\omega)&=\frac{1}{\sqrt{2\pi}}\left(\int_{-\infty}^{-T}0\cdot e^{-i\omega t}dt+\int_{-T}^{T}A\cos\omega_{0}t\cdot e^{-i\omega t}dt+\int_{T}^{\infty}0\cdot e^{-i\omega t}dt\right) \\
&=\frac{A}{\sqrt{2\pi}}\int_{-T}^{T}\frac{e^{i\omega_{0}t}+e^{-i\omega_{0}t}}{2}e^{-i\omega t}dt \\
&=\frac{A}{2\sqrt{2\pi}}\left(\int_{-T}^{T}e^{-i(\omega-\omega_{0})t}dt+\int_{-T}^{T}e^{-i(\omega+\omega_{0})t}dt\right) \\
&=\frac{A}{2\sqrt{2\pi}}\left(\left[\frac{e^{-i(\omega-\omega_{0})t}}{-i(\omega-\omega_{0})}\right]_{-T}^{T}+\left[\frac{e^{-i(\omega+\omega_{0})t}}{-i(\omega+\omega_{0})}\right]_{-T}^{T}\right) \\
&=\frac{Ai}{2\sqrt{2\pi}}\left\{\frac{e^{-i(\omega-\omega_{0})T}-e^{i(\omega-\omega_{0})T}}{\omega-\omega_{0}}+\frac{e^{-i(\omega+\omega_{0})T}-e^{i(\omega+\omega_{0})T}}{\omega+\omega_{0}}\right\} \\
&=\frac{Ai}{2\sqrt{2\pi}}\left[\frac{-2i\sin(\omega-\omega_{0})T}{\omega-\omega_{0}}+\frac{-2i\sin(\omega+\omega_{0})T}{\omega+\omega_{0}}\right] \\
&=\frac{A}{\sqrt{2\pi}}\left[\frac{\sin(\omega+\omega_{0})T}{\omega+\omega_{0}}+\frac{\sin(\omega-\omega_{0})T}{\omega-\omega_{0}}\right] \label{矩形cosのフーリエ変換} \tag{4}
\end{align}
よって、求めるフーリエ変換は
\begin{align}
\boxed{F(\omega)= \frac{A}{\sqrt{2\pi}}\left[\frac{\sin(\omega+\omega_{0})T}{\omega+\omega_{0}}+\frac{\sin(\omega-\omega_{0})T}{\omega-\omega_{0}}\right] } \label{reikai}\tag{5}
\end{align}
となる。
\(F(\omega)\)のグラフを描くと下図のようになる。
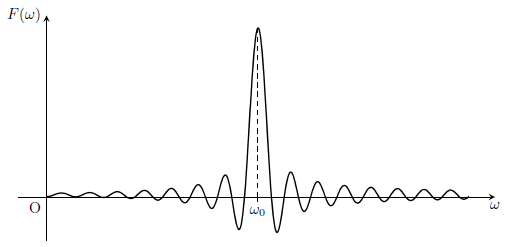
図を見ると、最大のピークが\(\omega=\omega_{0}\)の位置にあることがわかる。
これは\(f(t)\)において、周波数が\(\omega_{0}\)の周期関数が占める割合が高いことを示している。
事実、もとの関数\(f(t)\)は\(-T\leq t \leq T\)の範囲で角周波数\(\omega_{0}\)の周期関数であったわけだから、この結果は的を射たものだと言える。
終わりに
時間の関数の場合、フーリエ変換によって関数の周波数成分を調べられることが分かったと思う。
このフーリエ変換の基本的な応用に「ノイズ除去」がある。
次回はフーリエ変換の実用的手法である高速フーリエ変換(FFT)を利用して、波形のノイズ除去をする様子を見せたいと思う。
END





コメント