【フーリエ解析】フーリエ級数～概要と例題～

　大学数学の1つであるフーリエ解析は、 簡単に言うと「フーリエ級数」と「フーリエ変換」という2つの数学的手法の総称と言える。

　本記事では、その1つであるフーリエ級数について扱う。

　詳細な議論は教科書に一任し、数ページ分の分量でさっと概要を掴めるように書こうと思う。
　(完全に私の備忘録的な記事。)

三角関数の積分公式

　本題に入る前に、今後の計算を楽にするために以下に三角関数の積分公式をまとめておく。

概要

　フーリエ級数は下記のように表せられる。

　ここで\(f(x)\)は\(-L<x\leq L\)で定義された周期\(2L\)の周期関数である。
　(ただし、\(f(x)\)は\(-\infty<x\leq \infty\)で連続な関数に限る。)

　すなわち(\ref{fourier1})は、周期関数は複素指数関数\(e^{-i\frac{k\pi}{L}x}\)の足し合わせで表現できることを示している。

　もっと言えば、 周期関数は三角関数の足し合わせで表現できることを示している。

　

　\(c_{k}\)はフーリエ係数と呼ばれ、フーリエ級数では各三角関数の振幅、すなわち各成分の大きさを表す。
　(フーリエ係数が0なら、それに対応する成分は含まれないことを示している。)

例題①

　実際に具体例で試してみる。

解説

　\(f(x)\)は全領域で滑らかな周期\(2\pi\)の周期関数である。

　よってフーリエ級数、およびフーリエ係数\(c_{k}\)は

\begin{align}
&f(x)=\sum_{k=-\infty}^{\infty}c_{k}e^{ikx}
&\left(\text{ただし}\,c_{k}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x) e^{-ikx} dx\right) \label{rei1ck}\tag{3}
\end{align}

となる。

　

　まず\(c_{0}\)を計算する。

\begin{align}
c_{0}&=\frac{1}{2\pi}\int_{-\pi}^{\pi}( \sin x+2\cos 3x ) dx \\
&=\frac{1}{2\pi}\left(\int_{-\pi}^{\pi}\sin x dx+ \int_{-\pi}^{\pi} 2\cos 3x dx \right) \\
&=0\qquad((\ref{cossinm})より) \label{rei1c0}\tag{4}
\end{align}

　

　続いて\(c_{k}\)を計算する。

\begin{align}
&&c_{k}=&\frac{1}{2\pi}\int_{-\pi}^{\pi}( \sin x+2\cos 3x ) e^{-ikx} dx \\
&&=&\frac{1}{2\pi}\int_{-\pi}^{\pi}( \sin x+2\cos 3x )(\cos kx-i\sin kx) dx \\
&&=&\frac{1}{2\pi}\left(\int_{-\pi}^{\pi}\sin x\cos kx dx+ \int_{-\pi}^{\pi} 2\cos 3x\cos kx dx \right) \\
&& &-\frac{i}{2\pi}\left(\int_{-\pi}^{\pi}\sin x\sin kx dx+\int_{-\pi}^{\pi}2\cos 3x\sin kx dx \right) \\
&&=& \frac{1}{\pi}\int_{-\pi}^{\pi}\cos 3x\cos kx dx -\frac{i}{2\pi}\int_{-\pi}^{\pi}\sin x\sin kx dx \qquad((\ref{cosmsinn})より) \label{rei1ck1}\tag{5}
\end{align}

　ここで(\ref{rei1ck1})の最右辺の積分部分を計算する。

　まず第1項の積分については、(\ref{cosmcosn})より

\begin{align}
\int_{-\pi}^{\pi}\cos 3x\cos kx dx =\begin{cases}
\pi &(k=\pm 3)\\
0 &(\text{otherwise})
\end{cases} \label{rei11kou}\tag{6}
\end{align}

となる。

　続いて第2項については、(\ref{sinmsinn})より

\begin{align}
\int_{-\pi}^{\pi}\sin x\sin kx dx=\begin{cases}
\pi &(k=1)\\
-\pi &(k=-1) \\
0 &(\text{otherwise})
\end{cases} \label{rei12kou}\tag{7}
\end{align}

となる。

　よって(\ref{rei11kou})と(\ref{rei12kou})の結果を(\ref{rei1ck1})に代入して整理すると、

\begin{align}
c_{k}=\begin{cases}
1 &(k=\pm 3) \\
\displaystyle{-\frac{i}{2}} &(k=1) \\
\displaystyle{\frac{i}{2}} &(k=-1) \\
0 &(\text{otherwise})
\end{cases} \label{rei1ck2}\tag{8}
\end{align}

となる。

　

　以上より、(\ref{rei1ck2})をフーリエ級数(\ref{rei1ck})に代入すれば、

\begin{align}
f(x)&=\sum_{k=-\infty}^{\infty}c_{k}e^{ikx} \\
&=-\frac{i}{2}e^{ix}+\frac{i}{2}e^{-ix}+e^{3ix}+e^{-3ix} \\
&=-\frac{i}{2}( e^{ix} – e^{-ix} )+ e^{3ix}+e^{-3ix} \\
&= -\frac{i}{2} \cdot 2i\sin x+2\cos3x \\
&= \sin x+2\cos3x \label{rei1kai}\tag{9}
\end{align}

となり、元の\(f(x)\)と一致する。

例題②

　例題①では全領域で滑らかな周期関数だったが、次のような部分的に滑らかでない周期関数も扱うことができる。

解説

　\(f(x)\)を図示すると下図のようになる。

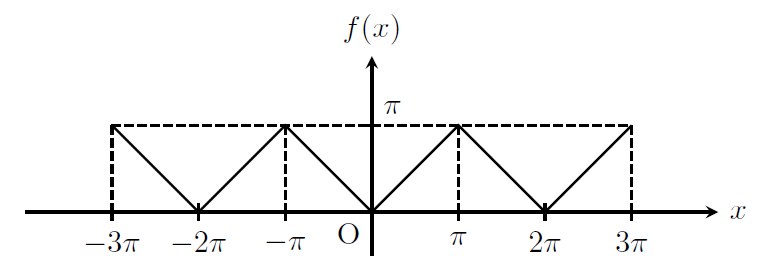
　以前執筆した、フーリエ級数の演習問題記事で登場した周期関数と同じである。

　フーリエ級数、およびフーリエ係数\(c_{k}\)は

\begin{align}
&f(x)=\sum_{k=-\infty}^{\infty}c_{k}e^{ikx}
&\left(\text{ただし}\,c_{k}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x) e^{-ikx} dx\right) \label{rei2ck}\tag{11}
\end{align}

となる。

　

　まず\(c_{0}\)を計算する。

\begin{align}
c_{0}&=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x) dx \\
&=\frac{1}{2\pi}\left( \int_{-\pi}^{0}(-x) dx+ \int_{0}^{\pi}x dx \right)\\
&=\frac{1}{2\pi}\left(\left[-\frac{1}{2}x^{2}\right]_{-\pi}^{0}+ \left[\frac{1}{2}x^{2}\right]_{0}^{\pi} \right)\\
&= \frac{1}{2\pi} \left(\frac{1}{2}\pi^{2}+ \frac{1}{2}\pi^{2} \right)\\
&=\frac{\pi}{2} \label{rei2c0}\tag{12}
\end{align}

　

　続いて\(c_{k}\)を計算する。

\begin{align}
c_{k}&=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x) e^{-ikx} dx \\
&= \frac{1}{2\pi} \left( \int_{-\pi}^{0}(-x)e^{-ikx} dx+ \int_{0}^{\pi}xe^{-ikx} dx \right) \\
&= \frac{1}{2\pi} \left( \int_{0}^{-\pi}xe^{-ikx} dx+ \int_{0}^{\pi}xe^{-ikx} dx \right) \label{rei2ck1}\tag{13}
\end{align}

　ここで\(a,b\)を定数として、定積分\(\displaystyle{ \int_{a}^{b}xe^{-ikx} dx }\)を計算する。

\begin{align}
\int_{a}^{b}xe^{-ikx} dx &=\left[-\frac{1}{ik} xe^{-ikx} \right]_{a}^{b}-\left(-\frac{1}{ik}\right)\int_{b}^{a} e^{-ikx} dx\\
&=\frac{i}{k}\left[xe^{-ikx}\right]_{a}^{b}+\frac{1}{ik}\left[-\frac{1}{ik}e^{-ikx}\right]_{a}^{b}\\
&=\frac{i}{k}\left[xe^{-ikx}\right]_{a}^{b}+\frac{1}{k^{2}}\left[e^{-ikx}\right]_{a}^{b} \label{exab}\tag{14}
\end{align}

　よって(\ref{exab})を利用すると、(\ref{rei2ck1})の最右辺の積分部分は

\begin{align}
\int_{0}^{-\pi}xe^{-ikx} dx&=\frac{i}{k}\left[xe^{-ikx}\right]_{0}^{-\pi}+\frac{1}{k^{2}}\left[e^{-ikx}\right]_{0}^{-\pi} \\
&=-\frac{i}{k}\pi e^{ik\pi}+\frac{1}{k^{2}}(e^{ik\pi}-1) \label{int-pi0}\tag{15}\\
\int_{0}^{\pi}xe^{-ikx} dx&=\frac{i}{k}\left[xe^{-ikx}\right]_{0}^{\pi}+\frac{1}{k^{2}}\left[e^{-ikx}\right]_{0}^{\pi} \\
&=\frac{i}{k}\pi e^{-ik\pi}+\frac{1}{k^{2}}(e^{-ik\pi}-1) \label{int0pi}\tag{16}
\end{align}

となるため、これらを(\ref{rei2ck1})に代入すると、

\begin{align}
c_{k}&=\frac{1}{2\pi}\left\{-\frac{i}{k}\pi e^{ik\pi}+\frac{1}{k^{2}}(e^{ik\pi}-1) + \frac{i}{k}\pi e^{-ik\pi}+\frac{1}{k^{2}}(e^{-ik\pi}-1) \right\} \\
&=\frac{1}{2\pi}\left\{ -\frac{i}{k}\pi (e^{ik\pi} – e^{-ik\pi})+\frac{1}{k^{2}}(e^{ik\pi}+e^{-ik\pi})-\frac{2}{k^{2}}\right\} \\
&=\frac{1}{2\pi}\left(-\frac{i}{k}\pi\cdot 2i\sin k\pi+\frac{1}{k^{2}}\cdot 2\cos k\pi-\frac{2}{k^{2}}\right) \\
&=\frac{1}{\pi k^{2}}(\cos k\pi -1)\quad(\sin k\pi=0より)\\
&=\frac{1}{\pi k^{2}}\left\{(-1)^{k} -1\right\} \label{rei2ck2}\tag{17}
\end{align}

となる。

　

　以上より、(\ref{rei2c0})と(\ref{rei2ck2})をフーリエ級数(\ref{rei2ck})を代入すると

\begin{align}
\boxed{f(x)=\frac{\pi}{2}+\frac{1}{\pi}\sum_{k=\pm 1}^{\pm\infty}\frac{(-1)^{k} -1}{k^{2}}e^{ikx}} \label{rei2kai1}\tag{18}
\end{align}

となる。

　フーリエ級数への展開は上記で終了でも良いが、ここからさらに下記のように変形できる。

\begin{align}
f(x)&= \frac{\pi}{2}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}e^{ikx}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{-k} -1}{(-k)^{2}}e^{-ikx} \\
&=\frac{\pi}{2}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}e^{ikx}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}e^{-ikx} \\
&=\frac{\pi}{2}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}(e^{ikx}+e^{-ikx}) \\
&=\frac{\pi}{2}+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}\cdot 2\cos kx \\
&=\frac{\pi}{2}+\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}\cos kx \quad\boxed{f(x)= \frac{\pi}{2}+\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{(-1)^{k} -1}{k^{2}}\cos kx} \label{rei2kai2}\tag{19}
\end{align}

　(\ref{rei2kai2})をさらに展開すると

\begin{align}
f(x)=\frac{\pi}{2}-\frac{4}{\pi}\left(\cos x+\frac{1}{3^{2}}\cos 3x+\frac{1}{5^{2}}\cos 5x+\cdots\right) \label{rei2kai3}\tag{20}
\end{align}

となる。

　(\ref{rei2kai3})の第1項まで、第2項までをそれぞれグラフ化すると下図のようになる。

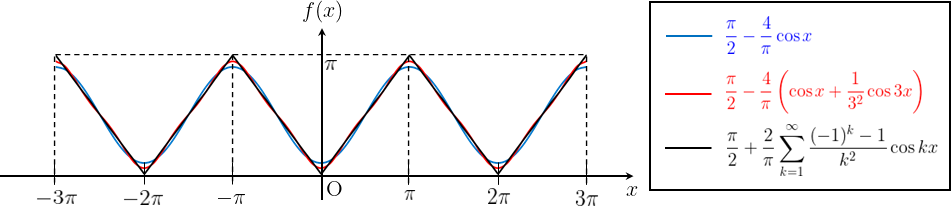
　項数が増えるにつれ、元の関数に近づいていく様子がわかると思う。

終わりに

　なんだかんだで長くなってしまった…

　次回はフーリエ解析のもう1つの手法である「フーリエ変換」を扱う。

　

　END