【G検定】Mini-Max法とαβ法～具体例でわかりやすい解説を試みてみた～

　G検定の勉強中、Mini-Max法とそれに関連する手法であるαβ法の解説を読んだが、これが結構わかりづらかった。

　複数の書籍と解説サイトを眺めながらようやく理解できたので、理解がある内になるべくわかりやすく、詳細に解説してみようと思う。

概要

　Mini-Max法は、ボードゲームにおける探索木を探索するために編み出された手法の1つであり、深さ優先探索で進める。

　ある局面の状態が自分にとってどれほど有利かを「スコア(コスト)」と呼ばれる値で評価し、以下のルールのもとで次の手を決定する。
　・自分(A)のターン→スコアが最大(自分に有利)になる手を選ぶ。
　・相手(B)のターン→スコアが最小(自分に不利)になる手を選ぶと仮定する。

　さらに、得られたスコアに基づいて余計な探索を減らすことも可能である。
　その手法がαβ法である。

具体例

　下図のような、3手先読みの探索木を例にαβ法を実施してみる。

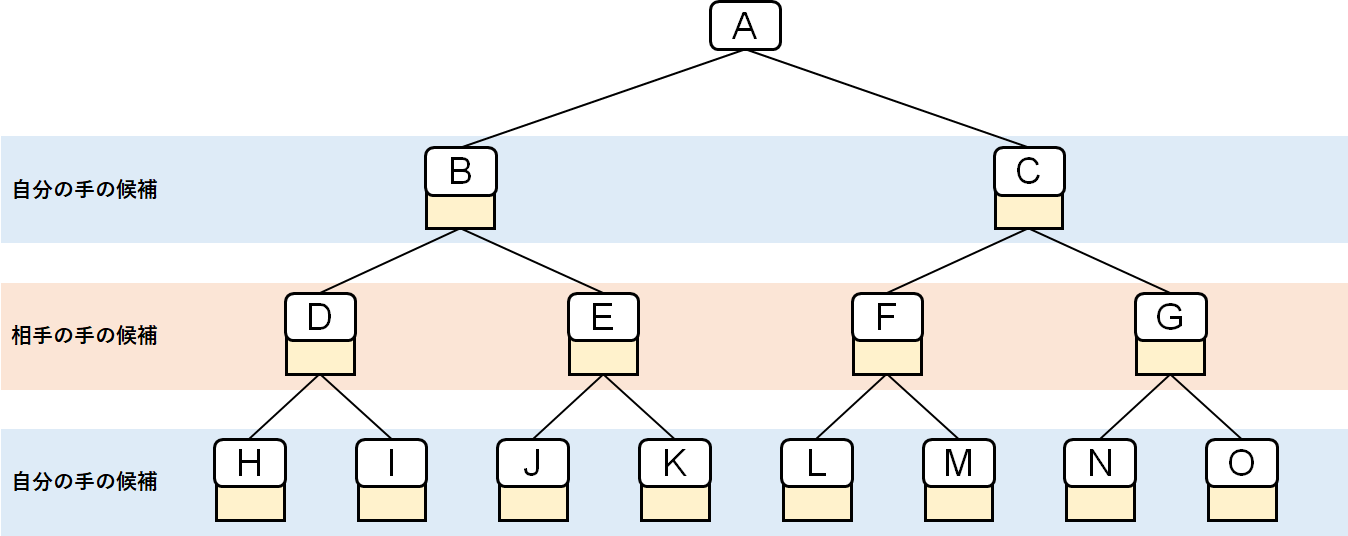
　盤面Aをスタートとし、先手が「自分」、後手が「相手」とする。
　Mini-Max法では深さ優先探索で進めるため、3手目の左端である盤面Hから右へ順番に探索していくとする。

　

　最初の探索では盤面Hまで進める。
　探索の結果、盤面Hでのスコアは3となった。
　このとき、盤面BとDのスコアも暫定的に3となる。

　

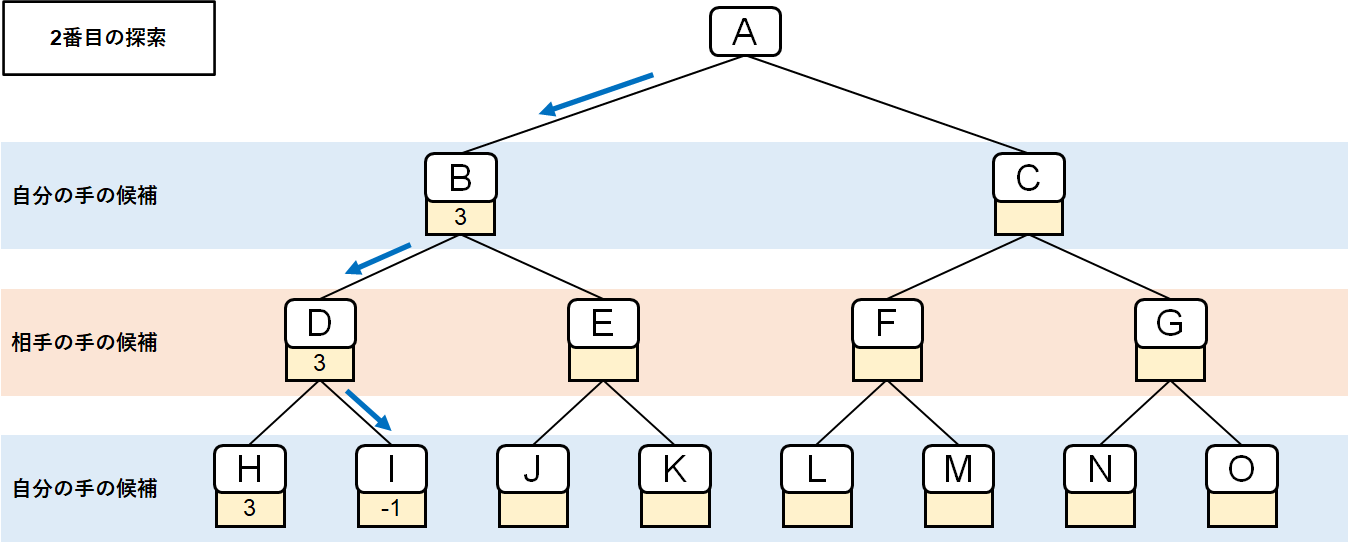
　2番目の探索は、盤面Iまでの探索となる。
　探索の結果、盤面Iのスコアは-1となった。
　このとき盤面Dのスコアは、盤面HとIのうち「自分」が選択する盤面のスコアと同値になる。
　「自分」はスコアが最大になるように手を打つので、「自分」は盤面Dが来たら盤面Hを選択するはずである。
　よって、盤面Dのスコアは盤面Hと同値である3で決定する。

　

　3番目の探索は、盤面Jまでの探索となる。
　探索の結果、盤面Jのスコアは5となった。
　このとき、盤面Eのスコアは暫定的に5となるが、盤面Bは3のままである。
　なぜなら、盤面Bのスコアは、盤面DとEのうち「相手」が選択する盤面のスコアと同値になるためである。
　「相手」はスコアが最小になるように手を打つので、「相手」は盤面Bが来たら今の段階では盤面Dを選択するはずである。

　そして「相手」が盤面Eを選択するためには、盤面Dのスコア3よりも盤面Eのスコアが小さくならなければならないが、実はこれはあり得ないことである。
　なぜなら、盤面Eのスコアは、盤面JとKのうち「自分」が選択する盤面のスコアと同値になるためである。
　「自分」はスコアが最大になるように手を打つので、「自分」は盤面Eが来たら、盤面JとKのうちスコアが高い方を選択するはずである。
　これはすなわち、盤面Eのスコアが5を下回ることはないことを意味する。
　(仮に盤面Kのスコアが1なら盤面Jのスコア5が、盤面Kのスコアが7ならそのスコア7がそのまま盤面Eのスコアになる。)

　よって3番目の探索の時点で、盤面Eのスコアは必ず5以上になることがわかったため、「相手」はスコアが3の盤面Dか、スコアが5以上の盤面Eの2択となる。
　先ほど説明した通り、「相手」はスコアが最小になるように手を打つので、上記の2択では「相手」はスコアが低い盤面Dを選択するはずである。

　よって、「相手」は盤面Bが来たら盤面Kのスコアに関わらず盤面Dを選択することが確定し、盤面Kへの探索をする必要がなくなる。
　そこで探索コストを削減するために、盤面Kへの探索をカット(無視)することにする。
　これを「βカット」と呼ぶ。

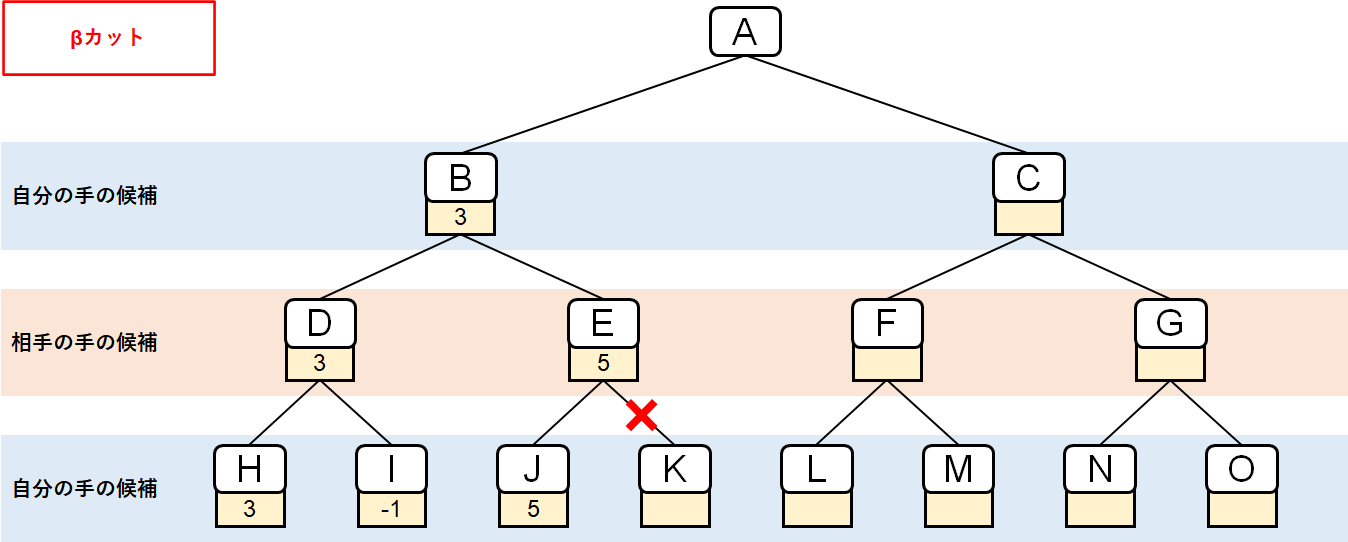
　βは盤面Eが取りうるスコアの上限値を表し、今回はβ値は3となる。
　(盤面Eのスコアが3を超えたらβカットが実行される。)

　

　よって4番目の探索は盤面Kへの探索をスキップし、盤面Lへの探索となる。

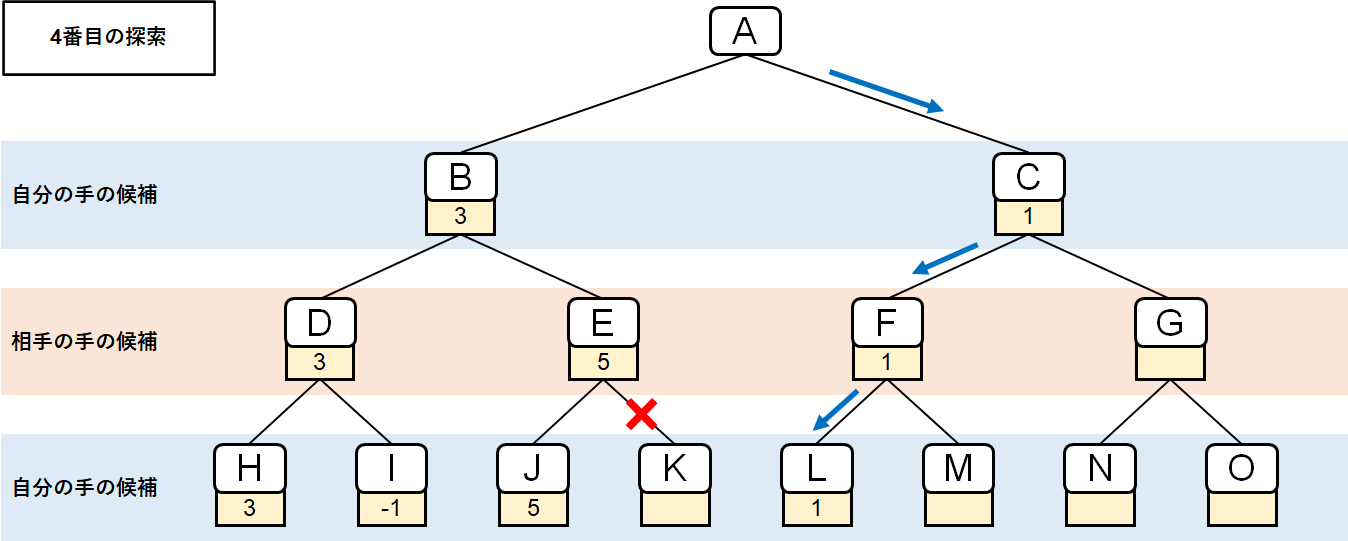
　探索の結果、盤面Lでのスコアは1となった。
　このとき、盤面CとFのスコアも暫定的に1となる。

　

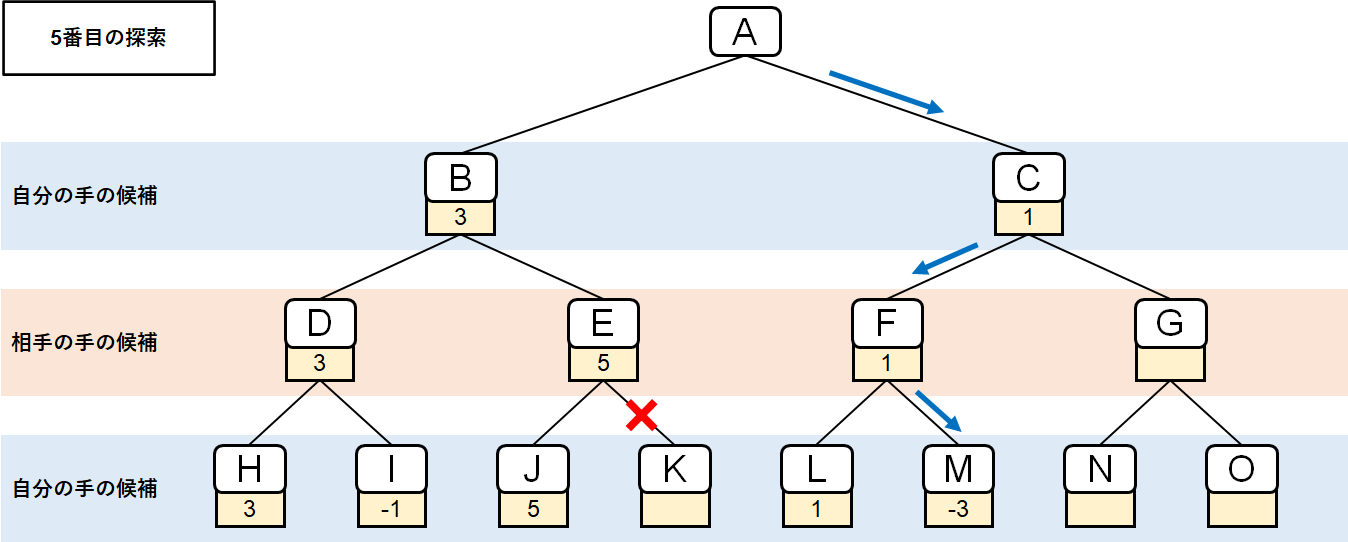
　5番目の探索は、盤面Mまでの探索となる。
　探索の結果、盤面Mのスコアは-3となった。
　このとき盤面Fのスコアは、盤面LとMのうち「自分」が選択する盤面のスコアと同値になる。
　「自分」はスコアが最大になるように手を打つので、「自分」は盤面Fが来たら盤面Lを選択するはずである。
　よって、盤面Fのスコアは盤面Lと同値である1で決定する。

　次は盤面Nへの探索になるが、実はこの探索、もとい盤面Gを経由する探索はもう実施する必要はない。
　なぜならこの時点で、「自分」の初手は盤面Bを選択することが確定したからだ。

　順を追って説明する。
　まず盤面Cのスコアは、盤面FとGのうち「相手」が選択する盤面のスコアと同値になる。
　「相手」はスコアが最小になるように手を打つので、「相手」は盤面Cが来たら、盤面FとGのうちスコアが低い方を選択するはずである。
　これはすなわち、盤面Cのスコアが1を上回ることはないことを意味する。
　(仮に盤面Gのスコアが4なら盤面Fのスコア1が、盤面Kのスコアが-2ならそのスコア-2がそのまま盤面Cのスコアになる。)

　よって5番目の探索の時点で、盤面Cのスコアは必ず1以下になることがわかったため、「自分」はスコアが3の盤面Bか、スコアが1以下の盤面Cの2択となる。
　先ほど説明した通り、「自分」はスコアが最大になるように手を打つので、上記の2択では「自分」はスコアが高い盤面Bを選択するはずである。

　このようにして、「自分」の初手は盤面Gのスコアに関わらず盤面Bを選択することが確定し、盤面Gへの探索をする必要がなくなる。
　そこで探索コストを削減するために、盤面Gへの探索をカット(無視)することにする。
　これを「αカット」と呼ぶ。

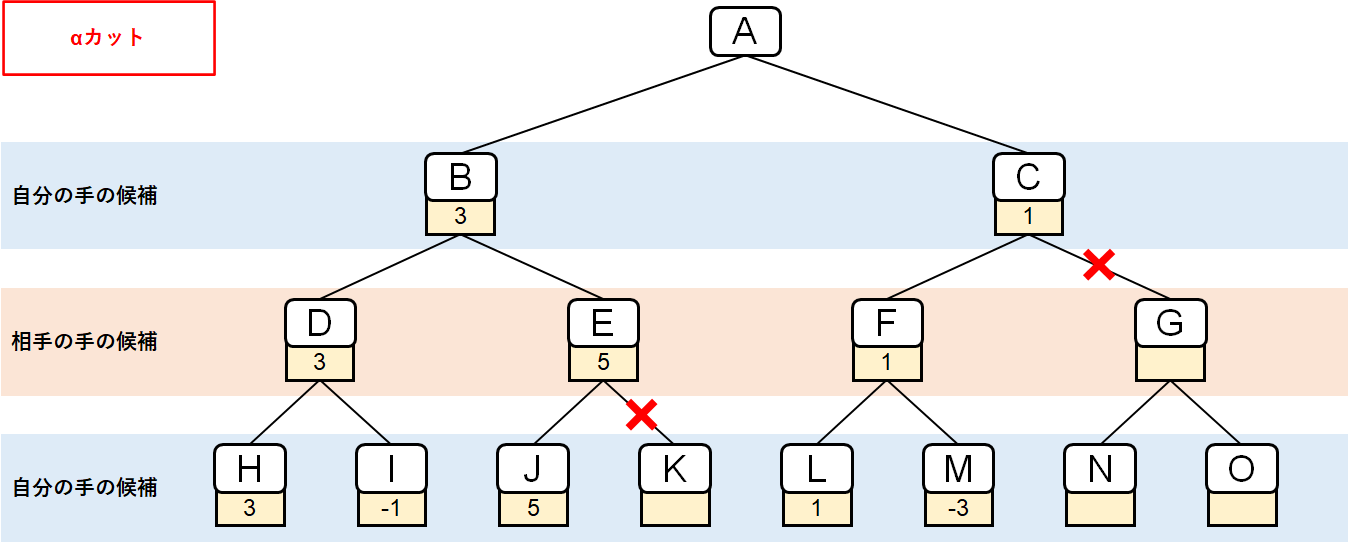
　αは盤面Cが取りうるスコアの下限値を表し、今回はβ値は3となる。
　(盤面Cのスコアが3を下回ったらαカットが実行される。)

　

　探索は以上で終了である。
　デフォルトのMini-Max法ではすべての手について探索するため、今回の例では探索数は8となる。
　しかしαβ法も併せて探索すれば、5回の探索で最善手を決定できる。

　条件が良ければ、αβ法で探索数を半減させることができると言われている。

終わりに

　なんだかんだ言いながら文字が多い解説になってしまった。

　ひとまずここで手打ちとするが、見返した時にやはりわかり辛かったら図を付け加えるなどして改善を試みようと思う。

　

　END