【AI】機械学習 by Python：分類編⑦～その他の手法①：線形SVM～

　前回

までで、ロジスティック回帰による分類問題の実装例を一通り見てきた。

　今回からロジスティック回帰以外の分類の手法をいくつか見ていく。
　まずは線形SVMだ。

仕組み

　線形SVM(サポートベクトルマシン)は、ロジスティック回帰と同じように線形分離可能な分類問題に用いられる手法である。

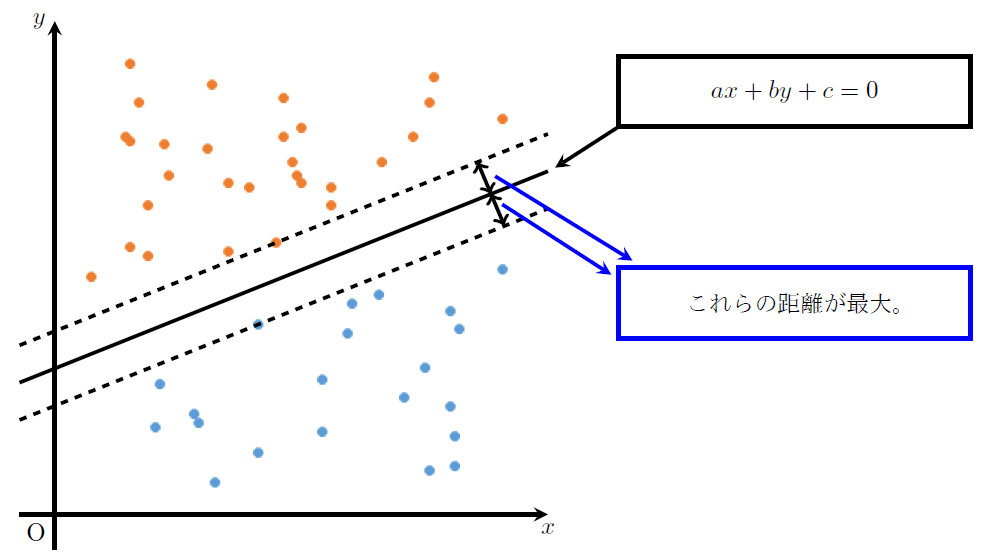
　二項分類の場合、下記の要領で分類する直線をひく。
①. 2つのクラスから、各クラスの境界線に最も近いデータ(クラス内で最も端に位置するデータ)を見つける。
②. ①で見つけた2つのデータからの距離が最大となり、かつ2つのクラスを分類できる直線をひく。

実装例

　前回

のロジスティック回帰で用いたデータセットをそのまま使って、線形SVMの実装例を示す。

実装例

# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.colors import ListedColormap
import sklearn
from sklearn.svm import LinearSVC
from sklearn import metrics

# データセットのインポート
file=pd.read_csv('logistic.csv',header=None)

# データの割り振り
X=file.iloc[:,0:2]
Y=file.iloc[:,2]

# データセットを学習データ（8割）とテストデータ（2割）に分割（random_stateは0）
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)
# 分割の確認
print('分割の確認：',X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)

# 学習実行
# インスタンスの作成
model=LinearSVC(max_iter=10000)
# モデルの作成
model.fit(X_train,Y_train)

# 直線の確認
# 切片
print('切片の値 = ', model.intercept_)
# 係数
print('係数の値 = ', model.coef_)

# 学習データからの予測値
pred_train = model.predict(X_train)
# テストデータからの予測値
pred_test = model.predict(X_test)

# 学習データを用いた分類モデルの評価
print('正解率(学習データ) = ', metrics.accuracy_score(Y_train, pred_train))
print('適合率(学習データ) = ', metrics.precision_score(Y_train, pred_train))
print('再現率(学習データ) = ', metrics.recall_score(Y_train, pred_train))
print('F値(学習データ) = ', metrics.f1_score(Y_train, pred_train))

# テストデータを用いた分類モデルの評価
print('正解率(テストデータ) = ', metrics.accuracy_score(Y_test, pred_test))
print('適合率(テストデータ) = ', metrics.precision_score(Y_test, pred_test))
print('再現率(テストデータ) = ', metrics.recall_score(Y_test, pred_test))
print('F値(テストデータ) = ', metrics.f1_score(Y_test, pred_test))

# データセットおよび直線の図示
plt.figure(figsize=(4,4))
plt.scatter(file.iloc[:,0], file.iloc[:,1],c=file.iloc[:,2], cmap=ListedColormap(['#FF0000', '#0000FF']))
plt.plot(file.iloc[:,0], -file.iloc[:,0]*model.coef_[0,0]/model.coef_[0,1]-model.intercept_[0]/model.coef_[0,1])
plt.show()

出力例

分割の確認： (160, 2) (40, 2) (160,) (40,)
切片の値 =  [-2.70071076]
係数の値 =  [[-0.00084609  0.54778661]]
正解率(学習データ) =  0.90625
適合率(学習データ) =  0.9080459770114943
再現率(学習データ) =  0.9186046511627907
F値(学習データ) =  0.9132947976878613
正解率(テストデータ) =  0.875
適合率(テストデータ) =  0.8125
再現率(テストデータ) =  0.8666666666666667
F値(テストデータ) =  0.8387096774193549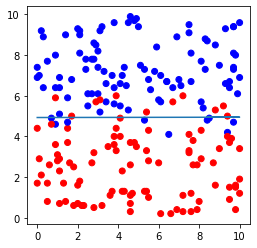

　実際にプログラムを実行したい場合は、下記ボタンよりcsvファイル「logistic.csv」をダウンロードしてプログラムの保存先に保存すること。

詳説

　詳説といっても、上の実装例はロジスティック回帰の実装例と9割5分同じだ。

　変わったのは下記の2か所だけである。

　

from sklearn.svm import LinearSVC

⇒線形SVMモデルのクラスである「LinearSVC」をインポートするためのコード。

　

model=LinearSVC(max_iter=10000)

⇒クラス「LinearSVC」を、「model」という名前のインスタンスに作り変えるコード。
　引数部の「max_iter」は計算の反復回数の最大値を指定するコードである。
　デフォルトでは反復回数の最大値は1000回だが、今回は訳あって10000回に設定してある。

エラー覚書

　反復回数の最大値を増やした理由をここに書いておく。

　最初は、私も反復回数の最大値を増やす予定はなく、下記のようにデフォルトのままインスタンス化をしようとした。

model=LinearSVC()

　しかし上記コードで実装すると、下記のようなエラーが発生した。

base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations."the number of iterations.", ConvergenceWarning)

　Pythonが「収束に失敗したので反復回数を増やしてくれ」と言ってきたわけだ。

　そこで仰せのままに反復回数を10倍に増やし、エラー表示が出ないようにしたのである。

次回予告

　次回は、線形分離不可能な2項分類問題を解く手法の1つである「非線形SVM」を扱う。

　

　END

　

　※追記
　「非線形SVM」の記事執筆。