大学に入学すると、物理の問題を解く上で非常に強力な武器を手に入れる。
それが微分方程式だ。
特に力学ではその強力さを体感できる。
ここでは、 空気抵抗を含む水平投射を例題に選定し、微分方程式で力学の問題が痛快に解けていく様子をご覧に入れよう。
問題
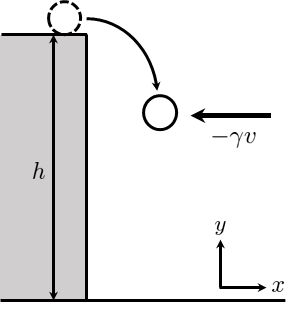
球は常に速度\(v\)に比例する空気抵抗力\(-\gamma v\)を受け(\(\gamma\)は粘性抗力係数)、水平右向き、鉛直上向きを正とする。
また重力加速度を\(g\)とする。
このとき、次の2つのグラフをそれぞれ描け。
・水平方向の変位\(x\)及び鉛直方向の変位\(y\)の時間変化
・球の運動の軌跡
ただし水平方向の初期位置は\(x=0\)としてよい。
また、球を質点とみなしてよい。
解答
まず水平方向の運動を考える。
水平方向にかかる力は空気抵抗力のみであるため、水平方向の運動方程式は
\begin{align}
m\frac{d^{2}x}{dt^{2}}=-\gamma\frac{dx}{dt} \tag{1}\label{suiheieq}
\end{align}
となる。ここで\(dx/dt=v_{x}\)として(\ref{suiheieq})を書き換えると、
\begin{align}
m\frac{dv_{x}}{dt}=-\gamma v_{x} \tag{2}\label{suiheieq2}
\end{align}
と書き換える。(\ref{suiheieq2})は一階の常微分方程式であり、変数分離の方法により解いていくと
\begin{gather}
\frac{1}{v_{x}}dv_{x}=-\frac{\gamma}{m}dt \\
\int\frac{1}{v_{x}}dv_{x}=-\frac{\gamma}{m}\int dt \\
\log |v_{x}|=-\frac{\gamma}{m}t+C_{1} \\
\log|v_{x}(t)|=\log e^{-\frac{\gamma}{m}t+C_{1}} \\
v_{x}(t)=D_{1}e^{-\frac{\gamma}{m}t} \tag{3}\label{suiheieq3}
\end{gather}
となる。ただし\(D_{1}=e^{c_{1}}\)であり、任意定数である。この\(D_{1}\)は初速度を使うと決定できる。水平方向の初速度は\(v_{x}(0)=v_{0}\)であるため、
\begin{align}
v_{x}(0)=D_{1}e^{-\frac{\gamma}{m}\cdot 0}=D_{1}=v_{0} \tag{4}
\end{align}
となり\(D_{1}=v_{0}\)であることがわかる。よって水平方向の速度は
\begin{align}
v_{x}(t)=v_{0}e^{-\frac{\gamma}{m}t} \tag{5}\label{suiheieq5}
\end{align}
と書ける。よって(\ref{suiheieq5})を時間\(t\)で積分すれば変位になるため、変位は
\begin{align}
x(t)=-\frac{mv_{0}}{\gamma}e^{-\frac{\gamma}{m}t}+C_{2} \tag{6} \label{suihei6}
\end{align}
となる。\(C_{2}\)は積分定数であるが、これは初期位置から決定できる。水平方向の初期位置は\(x=0\)であるため、
\begin{gather}
x(0)=-\frac{mv_{0}}{\gamma}e^{-\frac{\gamma}{m}\cdot 0}+C_{2}=-\frac{mv_{0}}{\gamma}+C_{2} =0 \\
C_{2}=\frac{mv_{0}}{\gamma} \tag{7}\label{suiheieq7}
\end{gather}
となる。よって(\ref{suiheieq7})を(\ref{suihei6})に代入すれば、水平方向の変位は
\begin{align}
x(t)=\frac{mv_{0}}{\gamma}\left(1-e^{-\frac{\gamma}{m}t} \right) \tag{8}
\end{align}
となり、これをグラフに描くと下図のようになる。
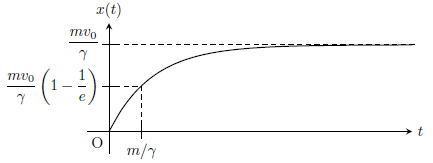
最初は右向きに進んでいくが、時間が十分経過すると\(x=mv_{0}/\gamma\)に落ち着く。空気抵抗により、水平方向の速度が減速する様子がはっきりと示されている。
続いて鉛直方向を考える。鉛直方向には空気抵抗力に加えて重力がかかるため、運動方程式は次式のようになる。
\begin{align}
m\frac{d^{2}y}{dt^{2}}=-\gamma\frac{dy}{dt}-mg \tag{9}\label{enchokueq}
\end{align}
ここで\(dy/dt=v_{y}\)とすると(\ref{enchokueq})は
\begin{align}
m\frac{dv_{y}}{dt}=-\gamma v_{y}-mg \tag{10}\label{enchoku2}
\end{align}
と書ける。(\ref{enchoku2})も一階の常微分方程式であり、変数分離法により解いていくと
\begin{gather}
\frac{dv_{y}}{dt}=-\frac{\gamma}{m}\left\{v_{y}+\frac{mg}{\gamma}\right\} \\
\frac{1}{v_{y}+(mg/\gamma)}dv_{y}=-\frac{\gamma}{m}dt \\
\int\frac{1}{v_{y}+(mg/\gamma)}dv_{y}=-\frac{\gamma}{m}\int dt \\
\log\left|v_{y}+\frac{mg}{\gamma}\right|=-\frac{\gamma}{m}t+C_{3} \\
\log\left|v_{y}+\frac{mg}{\gamma}\right|=\log e^{-\frac{\gamma}{m}t+C_{3}} \\
\left|v_{y}(t)+\frac{mg}{\gamma}\right|=e^{-\frac{\gamma}{m}t+C_{3}} \\
v_{y}(t)=D_{2}e^{-\frac{\gamma}{m}t }-\frac{mg}{\gamma} \tag{11}\label{enchoku3}
\end{gather}
となる。ここで\(D_{2}=e^{C_{3}}\)は任意定数であり、\(D_{2}\)は初速度から決定できる。鉛直方向の初速度は\(v_{y}(0)=0\)であるため
\begin{align}
v_{y}(0)=D_{2}e^{-\frac{\gamma}{m}\cdot 0 }-\frac{mg}{\gamma}=D_{2}-\frac{mg}{\gamma}=0 \tag{12}
\end{align}
となり\(D_{2}=mg/\gamma\)であることがわかる。よって鉛直方向の速度は
\begin{align}
v_{y}(t)=\frac{mg}{\gamma}\left(e^{-\frac{\gamma}{m}t}-1\right) \tag{13}\label{enchoku13}
\end{align}
と書ける。よって(\ref{enchoku13})を積分すれば変位になるため、変位は
\begin{align}
y(t)=\frac{mg}{\gamma}\left(-\frac{m}{\gamma}e^{-\frac{\gamma}{m}t}-t\right)+C_{4} \tag{14}\label{enchoku14}
\end{align}
となる。\(C_{4}\)は積分定数であるが、これは初期位置から決定できる。鉛直方向の初期位置は\(y=h\)であるため、
\begin{gather}
y(0)=\frac{mg}{\gamma}\left(-\frac{m}{\gamma}e^{-\frac{\gamma}{m}\cdot 0}-0\right)+C_{4}=-\frac{m^{2}g}{\gamma^{2}}+C_{4}=h \\
C_{4}=\frac{m^{2}g}{\gamma^{2}}+h \tag{15}\label{enchoku15}
\end{gather}
となる。よって(\ref{enchoku15})を(\ref{enchoku14})に代入すれば、鉛直方向の変位は
\begin{align}
y(t)=\frac{m^{2}g}{\gamma^{2}}\left(1-e^{-\frac{\gamma}{m}t}\right)-\frac{mg}{\gamma}t+h \tag{16}\label{enchoku16}
\end{align}
となり、これをグラフに描くと下図のようになる。
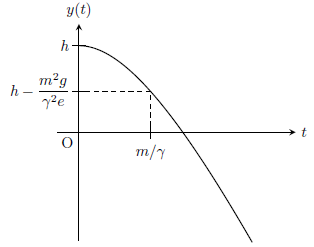
十分時間が経過すると(\(t \to \infty \))、\(y(t)=-(mg/\gamma)t+(m^{2}g/\gamma^{2})+h\)となり、球は鉛直下向きに等速落下する。このときの速度\(v_{\text{e}}=-mg/\gamma\)がいわゆる終端速度と呼ばれるものである。
以上より、球の運動の軌跡は下図のようになる。
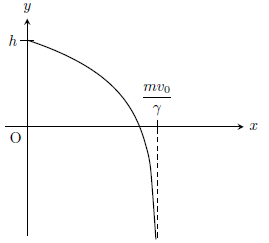
最後に
空気抵抗による水平方向の運動の抑止、およびその位置や速度までが、2つの微分方程式を解くだけでわかってしまう。
これが高校物理だったらおそらく「空気抵抗を受けたときの水平方向の速度および変位の公式」みたいな感じのただの暗記項目として与えられるだけになってしまい、全く面白みがないものになっていたかもしれない。
だが、微分方程式を解く方法を知ってしまえば、そんなものを覚える必要はない。
三角関数でいう加法定理さえ覚えてしまえば他の公式を導き出せるような、そんな体験を物理でも味わえるわけだ。
今後もこういった感じで、特に私が面白く感じた問題を中心に記事に書いて紹介していきたいと思う。
END
※追記
力学の王道、単振動の問題を取り上げてみた。





コメント
鉛直方向の運動方程式は
下向きを正として、
ma=mg-kv (kは比例定数)
のように、空気抵抗と重力の向きは逆にならないのですか?
教えてください
おそらく「重力と空気抵抗は向きが逆なのに、なぜ運動方程式上ではともに符号がマイナスがついているのか?」という疑問を抱いての質問だと思います(違っていたらごめんなさい)。
空気抵抗は物体が動く方向(速度の方向)に対して必ず逆向きの力になるので、どのように座標系をとっても必ずマイナスの符号が付きます。
もっとしっかり考えるなら、各物理量の正負を見ていく必要があります。
まず重力ですが、
・m>0かつg>0
・重力は鉛直下向きにかかる力(マイナス方向の力)
・今は鉛直上向きが正
なので、「mg」につく符号はマイナスになり、「-mg」トータルでもマイナスの値になります。
そして空気抵抗ですが
・γ>0かつv<0
・空気抵抗は鉛直上向きにかかる力(プラス方向の力)
・今は鉛直上向きが正
なので、「γv」につく符号はマイナスになり、「-γv」トータルではプラスの値になります。
鉛直上向きを正として落下運動を考えるときは「v<0」となるのがポイントです。
ちなみに鉛直下向きを正とすれば、仰る通りma=mg-kvで正解です。
小球が地面に落ちる、すなわちy(t)=0を解くことは可能なのでしょうか。
式(16)の右辺が0となるときの時間tを求めたい、ということでしょうか?
この場合だと解析的に解くことはできません。