本記事では、条件付き確率が絡む「ベイズの定理」について解説する。
G検定でも頻出の定理だが、参考書では定理だけ示され、導出過程などはすっ飛ばされることが多い。
本記事では自分が理解した範囲で、条件付き確率の定義からスタートし、導出、応用まで扱う。
条件付き確率
まずは「条件付き確率」とはそもそも何か、という話から。
結論から先に述べると、条件付き確率とは下記のようなものだ。
条件付き確率
2種類の事象AとBが起こる試行があり、事象Bの起こる確率を\(P(B)\)、AとBの同時確率を\(P(A\cap B)\)としたとき、事象Bが起こるという条件の下で事象Aが起きる条件付き確率\(P(A|B)\)は次式で定義される。
\begin{align}
P(A|B)=\frac{P(A\cap B)}{P(B)} \label{acbpro2}\tag{1}
\end{align}
表記の仕方にはいくつか種類があり、同時確率\(P(A\cap B)\)を\( P(A,B)\)、条件付き確率を \(P(A|B)\) を \(P_{B}(A)\)と表したりする。
ここで、上式が意味するところをもう少し掘り下げて考えてみる。
起こりうる全事象の場合の数を\(X(U)\)とし、そのうち事象Aが起こる場合の数を\(X(A)\)、事象Bが起こる場合の数を\(X(B)\)、事象Aかつ事象Bとなる場合の数を\(X(A\cap B)\)とする。
このとき、試行の結果、事象Aとなる確率\(P(A)\)、事象Bとなる確率\(P(B)\)、 事象Aかつ事象Bとなる確率\(P(A\cap B)\)はそれぞれ次式で与えられる。
\begin{gather}
P(A)=\frac{X(A)}{X(U)} \label{Apro}\tag{2}\\
P(B)=\frac{X(B)}{X(U)} \label{Bpro}\tag{3}\\
P(A\cap B)=\frac{X(A\cap B)}{X(U)} \label{AcBpro}\tag{4}
\end{gather}
ここで、事象Aが起きる確率を求める際に、「事象Bが起きた上で」という条件を加えることにする。
すなわち、事象Bが起きた上で事象Aが起きる確率を考えるのである。
このとき、事象Bが起きていることは既にわかっているので、計算対象を事象Bを含む場合に限定することができる。
またこのとき、事象Aとなる場合の数は、事象Bかつ事象Aとなる場合の数\(X(A\cap B)\)に等しい。
以上より、事象Bが起きた上で事象Aが起こる確率を\(P(A|B)\)とすると、
\begin{align}
P(A|B)=\frac{X(A\cap B)}{X(B)} \label{pab1}\tag{5}
\end{align}
となる。
よって(\ref{pab1})に(\ref{Bpro})、(\ref{AcBpro})を代入すると、
\begin{align}
P(A|B)=\frac{P(A\cap B)X(U)}{P(B)X(U)}=\frac{ P(A\cap B) }{P(B)}
\end{align}
となり、(\ref{acbpro2})と一致する。
ベイズの定理
さて準備が整ったところで、ベイズの定理を見てみる。
ベイズの定理
2種類の事象AとBが起こる試行があり、事象Aの起こる確率を\(P(A)\)、事象Bの起こる確率を\(P(B)\)、AとBの同時確率を\(P(A\cap B)\)、事象Aが起こるという条件の下で事象Bが起きる条件付き確率を\(P(B|A)\)としたとき、事象Bが起こるという条件の下で事象Aが起きる条件付き確率\(P(A|B)\)は次式で表される。
\begin{align}
P(A|B)=\frac{P(B|A)P(A)}{P(B)} \label{bayes}\tag{2}
\end{align}
証明は(\ref{acbpro2})を利用すればよい。
\(P(B|A)\)は(\ref{acbpro2})より
\begin{align}
P(B|A)=\frac{P(A\cap B)}{P(A)} \label{bcapro2}\tag{3}
\end{align}
となるため、(\ref{bcapro2})を変形して(\ref{acbpro2})に代入すれば(\ref{bayes})となる。
例題1:サイコロ
ここでまず条件付き確率を扱った例題を解いてみる。
例題1
一様な6面サイコロを2回振る試行を考える。
このとき、次の問いに答えよ。
(1) 2回の試行の内のいずれかで5の目が出る確率を求めよ。
(2) 出た目の合計が7であることがわかっているとき、2回の試行の内のいずれかで5の目が出る確率を求めよ。
解説
(1)
1回目の試行で出た目を\(j_{1}\)、2回目の試行で出た目を\(j_{2}\)とすると、2回の試行の内のいずれかで5の目が出る事象は\((j_{1},j_{2})=(1,5), (5,1), (2,5), (5,2), (3,5), (5,3), (4,5), (5,4), (5,5), (6,5), (5,6)\)の11通りである。
全事象は36通り存在するため、求める確率は\(\boxed{\displaystyle{\frac{11}{36}}}\)となる。
(2)
出た目の合計が7である事象は\((j_{1},j_{2})=(1,6), (6,1), (2,5), (5,2), (3,4), (4,3)\)の6通りである。
これらの内で5の目が出る事象は\((j_{1},j_{2})=(2,5), (5,2)\)の2通りであるため、求める確率は\(\displaystyle{\frac{2}{6}=\frac{1}{3}}\)より\(\boxed{\displaystyle{\frac{1}{3}}}\)となる。
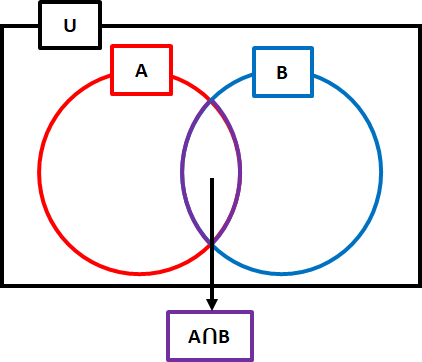
本問をベン図で描画すると右図のようになる。
今回はAが「2回の試行の内のいずれかで5の目が出る事象」、Bが「出た目の合計が7である事象」である。

例題2:感染検査
続いてベイズの定理を利用した、より実践的な例題を扱う。
頻出なのは以下に示すような、病原菌やウイルスの感染検査の有効性を問う問題だ。
例題2
母集団に属する人がウイルスAに感染する確率が0.1%であるとする。
このウイルスAに対する検査が存在し、ウイルスAに感染している人がこの検査を受けると95%の確率で陽性を示し、逆にウイルスAに感染していない人がこの検査を受けると1%の確率で陽性を示すことが分かっている。
このとき、検査の陽性者が実際にウイルスAに感染している確率を求めよ。
解説
今回知りたいのは「検査の陽性者の中でのウイルスAの感染者の割合」である。
よって陽性者を母集団とした感染確率を求めればよく、これは条件付き確率\(P(感|陽)\)に他ならない。
よってベイズの定理より
\begin{align}
P(感|陽)=\frac{P(陽|感)P(感)}{P(陽)} \label{病気1}\tag{4}
\end{align}
となるため、\(P(陽|感),P(感),P(陽)\)の3つが分かれば\(P(感|陽)\)が判明する。
まず\(P(陽|感)\)だが、これはウイルスAの感染者の中で検査結果が陽性になる確率であるため、\(P(陽|感)=95\%=0.95\)となる。
続いて\(P(感)\)だが、これは母集団'(全体)に対する感染確率であるため\(P(感)=0.1\%=0.001\)となる。
最後に\(P(陽)\)だが、これは母集団(全体)で検査結果が陽性になる確率であるため、感染者でありかつ陽性者である確率\(P(陽\cap 感)\)と、非感染者かつ陽性者である確率\(P(陽\cap 非感)\)の総和で表される。
よって
\begin{align}
P(陽)&= P(陽\cap 感) + P(陽\cap 非感) \\
&=P(陽|感)P(感) + P(陽|非感)P(非感)\quad(条件付き確率の定義(\ref{acbpro2})より。) \\
&=(0.95\times 0.001)+\{0.01\times(1-0.001)\}\\
&=0.01094 \label{病気2}\tag{5}
\end{align}
となる。
以上の結果を(\ref{病気1})に代入すれば
\begin{align}
P(感|陽)=\frac{0.95\times 0.001}{0.01094}=0.0868
\end{align}
となり、検査の陽性者が実際にウイルスAに感染している確率は約\(\boxed{8.7\%}\)となる。
事前確率と事後確率
ここで先ほどの例題から、ベイズの定理で何ができるのかをもう少し詳しく見ていく。
問題を解く前に、自分たちが把握していたのは母集団に対する感染確率\(P(感)\)だった。
この\(P(感)\)を把握した上で、「病気検査を実施して陽性となった」という条件が加わった上での感染確率\(P(感|陽)\)を求めるのがこの問題の目的だった。
これは、条件なしの確率\(P(感)\)に新たな情報(条件)が加わり、更新された確率\(P(感|陽)\)を求める問題とも言い換えることができる。
この情報が加わる前の確率\(P(感)\)を事前確率、情報が与えられて更新された確率\(P(感|陽)\)を事後確率と呼ぶ。
終わりに
事前確率、事後確率、ベイズの定理はG検定でも出題される事項だが、自分の受験時の理解度は中途半端だった。
ちゃんと理解するにはそれなりに時間をかける必要があったが、わかってくると面白い。
いっそのこと、高校数学から確率を勉強し直してみるか…?
END




コメント