確率変数が離散値を取る確率分布を離散型確率分布と呼ぶ。
その離散確率分布の代表格に、ベルヌーイ分布、カテゴリカル分布、二項分布、多項分布の4つがある。
これら4つを全て暗記しようとすると大変だが、実はこれら4つには関係性があり、多項分布さえ把握しておけば他の3つを導出することができる。
本記事では4つの離散型確率分布の関係性に着目し、多項分布から他の3つの分布を導出する方法を示す。
多項分布
概要
多項分布(マルチヌーイ分布)の確率関数は次式で与えられる。
多項分布(マルチヌーイ分布)
\begin{gather}
f(x_{j};p_{j})=N!\prod_{j=1}^{k}\frac{p_{j}^{x_{j}}}{x_{j}!} \label{多項分布表式}\tag{1}\\
\left(\text{ただし}\sum_{j=1}^{k}x_{j}=N,\,\sum_{j=1}^{k}p_{j}=1\right) \label{多項分布条件}\tag{2}
\end{gather}
確率\(p_{j}\)で事象\(E_{j}\)が起こる試行を \(N\)回繰り返したとき、各事象が\(x_{j}\)回起きる確率(「事象 \( E_{1}\)が \( x_{1}\)回」かつ「事象 \( E_{2}\)が \( x_{2}\)回」かつ・・・「事象 \( E_{k}\)が \( x_{k}\)回」起きる確率)は多項分布に従う。
例
最も身近な例がサイコロであろう。
\(k\)個の面を持つサイコロ(正多面体でも歪でもよい)を振るという試行を\(N\)回繰り返したとき、各面が\(x_{j}\)回出る確率(「1の面が\(x_{1}\)回」かつ「2の面が\(x_{2}\)回」かつ・・・「\(k\)の面が\(x_{k}\)回」出る確率)は多項分布に従う。

例題
例題1
各面が出る確率が以下の\(p_{j}\)で与えられる5面の歪なサイコロを振る試行を考える。
| 面 | 1 | 2 | 3 | 4 | 5 |
| \(p_{j}\) | \(\displaystyle{\frac{1}{3}}\) | \(\displaystyle{\frac{2}{9}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{9}}\) |
このサイコロを6回振り、各面が出た回数を\(x_{j}\)としたとき、次の3つの結果になる確率を求めよ。
ただし、求める確率は多項分布に従うとする。
| \(x_{1}\) | \(x_{2}\) | \(x_{3}\) | \(x_{4}\) | \(x_{5}\) | |
|---|---|---|---|---|---|
| 結果1 | 2 | 1 | 1 | 1 | 1 |
| 結果2 | 4 | 2 | 0 | 0 | 0 |
| 結果3 | 0 | 0 | 2 | 2 | 2 |
解説
結果1について、求める確率を\(f_{1}(x_{j},p_{j})\)とすると(\ref{多項分布表式})より
\begin{align}
f_{1}(x_{j},p_{j})&=6!\prod_{j=1}^{5}\frac{p_{j}^{x_{j}}}{x_{j}!}\\
&=6!\cdot\frac{1}{2!}\left(\frac{1}{3}\right)^{2}\cdot\frac{1}{1!}\left(\frac{2}{9}\right)^{1}\cdot\frac{1}{1!}\left(\frac{1}{6}\right)^{1}\cdot\frac{1}{1!}\left(\frac{1}{6}\right)^{1}\cdot\frac{1}{1!}\left(\frac{1}{9}\right)^{1}\\
&=\frac{20}{729}\simeq \boxed{2.74\times10^{-2}}
\end{align}
となる。
結果2について、求める確率を\(f_{2}(x_{j},p_{j})\)とすると(\ref{多項分布表式})より
\begin{align}
f_{2}(x_{j},p_{j})&=6!\prod_{j=1}^{5}\frac{p_{j}^{x_{j}}}{x_{j}!}\\
&=6!\cdot\frac{1}{4!}\left(\frac{1}{3}\right)^{4}\cdot\frac{1}{2!}\left(\frac{2}{9}\right)^{2}\cdot\frac{1}{0!}\left(\frac{1}{6}\right)^{0}\cdot\frac{1}{0!}\left(\frac{1}{6}\right)^{0}\cdot\frac{1}{0!}\left(\frac{1}{9}\right)^{0}\\
&=\frac{20}{2187}\simeq \boxed{9.14\times10^{-3}}
\end{align}
となる。
結果3について、求める確率を\(f_{3}(x_{j},p_{j})\)とすると(\ref{多項分布表式})より
\begin{align}
f_{3}(x_{j},p_{j})&=6!\prod_{j=1}^{5}\frac{p_{j}^{x_{j}}}{x_{j}!}\\
&=6!\cdot\frac{1}{0!}\left(\frac{1}{3}\right)^{0}\cdot\frac{1}{0!}\left(\frac{2}{9}\right)^{0}\cdot\frac{1}{2!}\left(\frac{1}{6}\right)^{2}\cdot\frac{1}{2!}\left(\frac{1}{6}\right)^{2}\cdot\frac{1}{2!}\left(\frac{1}{9}\right)^{2}\\
&=\frac{5}{5832}\simeq \boxed{8.57\times10^{-4}}
\end{align}
となる。
それぞれの結果を比較すると、結果1のように「出る目がばらけている」かつ「出る確率が高い目が出る回数が多い」場合は確率が高くなることがわかる。
また結果3のように、出る確率が低い目が出る回数が多い場合は確率が低くなる。
カテゴリカル分布
概要
ここで、多項分布(\ref{多項分布表式})において\(N=1\)となる場合を考える。
すなわち、試行回数を1回だけにするのである。
\begin{align}
f(x_{j};p_{j})=1!\prod_{j=1}^{k}\frac{p_{j}^{x_{j}}}{x_{j}!} \label{カテゴリカル1}\tag{3}
\end{align}
このとき、事象が起きる回数\(x_{j}\)は0または1となるため、\(x_{j}!=1\)となる。
よって(\ref{カテゴリカル1})は
\begin{align}
f(x_{j};p_{j})=1!\prod_{j=1}^{k}\frac{p_{j}^{x_{j}}}{1!}
=\prod_{j=1}^{k}p_{j}^{x_{j}}
\end{align}
となる。これがカテゴリカル分布の確率関数である。
カテゴリカル分布
\begin{align}
f(x_{j};p_{j})=\prod_{j=1}^{k}p_{j}^{x_{j}} \label{カテゴリカル表式}\tag{4}
\end{align}
例
\(k\)個の面を持つサイコロ(正多面体でも歪でもよい)を1回だけ振ったとき、各面が\(x_{j}\)回出る確率(「1の面が\(x_{1}\)回」かつ「2の面が\(x_{2}\)回」かつ・・・「\(k\)の面が\(x_{k}\)回」出る確率)はカテゴリカル分布に従う。

例題
例題2
\(j\)の面が出る確率\(p_{j}\)が異なる、以下の2つのサイコロをそれぞれ1回振る試行を考える。
| サイコロ | \(p_{1}\) | \(p_{2}\) | \(p_{3}\) | \(p_{4}\) | \(p_{5}\) | \(p_{6}\) |
|---|---|---|---|---|---|---|
| サイコロ1 | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) |
| サイコロ2 | \(\displaystyle{\frac{1}{4}}\) | \(\displaystyle{\frac{2}{9}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{6}}\) | \(\displaystyle{\frac{1}{9}}\) | \(\displaystyle{\frac{1}{12}}\) |
このとき、サイコロ1で2の面が出る確率、サイコロ2で6の面が出る確率をそれぞれカテゴリカル分布の確率関数から計算して求め、上の表の値と一致することを確認せよ。
解説
サイコロ1について、求める確率を\(f_{1}(x_{j},p_{j})\)とすると(\ref{カテゴリカル表式})より
\begin{align}
f_{1}(x_{j};p_{j})=\prod_{j=1}^{6}p_{j}^{x_{j}}=\left(\frac{1}{6}\right)^{0}\cdot\left(\frac{1}{6}\right)^{1}\cdot\left(\frac{1}{6}\right)^{0}\cdot\left(\frac{1}{6}\right)^{0}\cdot\left(\frac{1}{6}\right)^{0}\cdot\left(\frac{1}{6}\right)^{0}=\boxed{\frac{1}{6}}
\end{align}
となる。
サイコロ2について、求める確率を\(f_{2}(x_{j},p_{j})\)とすると(\ref{カテゴリカル表式})より
\begin{align}
f_{2}(x_{j};p_{j})=\prod_{j=1}^{6}p_{j}^{x_{j}}=\left(\frac{1}{4}\right)^{0}\cdot\left(\frac{2}{9}\right)^{0}\cdot\left(\frac{1}{6}\right)^{0}\cdot\left(\frac{1}{6}\right)^{0}\cdot\left(\frac{1}{9}\right)^{0}\cdot\left(\frac{1}{12}\right)^{1}=\boxed{\frac{1}{12}}
\end{align}
となる。
二項分布
概要
続いて、多項分布(\ref{多項分布表式})において\(k=2\)となる場合を考える。
すなわち事象の種類が2種類のみの場合である。
\begin{align}
f(x_{j};p_{j})&=N!\prod_{j=1}^{2}\frac{p_{j}^{x_{j}}}{x_{j}!}=N!\cdot\frac{p_{1}^{x_{1}}}{x_{1}!}\cdot\frac{p_{2}^{x_{2}}}{x_{2}!}\label{二項分布1}\tag{5}
\end{align}
ここで、\(x_{1}=x, p_{1}=p\)と置くと、(\ref{多項分布条件})より\(x_{2}=N-x, p_{2}=1-p\)とおける。
これを(\ref{二項分布1})に代入すると
\begin{align}
f(x_{j};p_{j})=N!\cdot\frac{p^{x}}{x!}\cdot\frac{(1-p)^{N-x}}{(N-x)!}=\frac{N!}{x!(N-x)!}p^{x}(1-p)^{N-x}={}_{N}\mathrm{C}_{x}\,p^{x}(1-p)^{N-x}
\end{align}
となる。これが二項分布の確率関数である。
二項分布
\begin{gather}
f(x_{j};p_{j})= {}_{N}\mathrm{C}_{x}\,p^{x}(1-p)^{N-x} \label{二項分布表式}\tag{6}
\end{gather}
例
多項分布ではサイコロだったが、これをコインに置き換えれば二項分布になる。
コイン(均質でも歪でもよい)を振るという試行\(N\)回繰り返したとき、「表面が\(x\)回」かつ「裏面が\(N-x\)回」出る確率は二項分布に従う。

例題
例題3
表面が出る確率が\(2/3\)、裏面が出る確率が\(1/3\)の歪なコインを振る試行を考える。
このコインを4回振ったとき、次の3つの結果になる確率を求めよ。
ただし、求める確率は二項分布に従うとする。
| 表が出た回数 | 裏が出た回数 | |
|---|---|---|
| 結果1 | 2 | 2 |
| 結果2 | 3 | 1 |
| 結果3 | 1 | 3 |
解説
表面が出た回数を\(x\)、表面が出る確率を\(p\)とする。
結果1について、求める確率を\(f_{1}(x;p)\)とすると(\ref{二項分布表式})より
\begin{align}
f_{1}(x;p)= {}_{4}\mathrm{C}_{2} \left(\frac{2}{3}\right)^{2}\left(1-\frac{2}{3}\right)^{2} =\frac{4!}{2!(4-2)!}\left(\frac{2}{3}\right)^{2}\left(\frac{1}{3}\right)^{2}=\boxed{\frac{8}{27}}
\end{align}
となる。
結果2について、求める確率を\(f_{2}(x;p)\)とすると(\ref{二項分布表式})より
\begin{align}
f_{2}(x;p)= {}_{4}\mathrm{C}_{3} \left(\frac{2}{3}\right)^{3}\left(1-\frac{2}{3}\right)^{1} =4\left(\frac{2}{3}\right)^{3}\left(\frac{1}{3}\right)^{1}= \boxed{ \frac{32}{81}}
\end{align}
となる。
結果3について、求める確率を\(f_{3}(x;p)\)とすると(\ref{二項分布表式})より
\begin{align}
f_{1}(x;p)= {}_{4}\mathrm{C}_{1} \left(\frac{2}{3}\right)^{1}\left(1-\frac{2}{3}\right)^{3} = 4\left(\frac{2}{3}\right)^{1}\left(\frac{1}{3}\right)^{3}= \boxed{ \frac{8}{81}}
\end{align}
となる。
それぞれ結果を比較すると、出る確率が高い面が出る回数が多ければ、ちゃんと確率も高くなっていることがわかる。
ベルヌーイ分布
概要
最後に、多項分布(\ref{多項分布表式})において\(N=1\)かつ\(k=2\)となる場合を考える。
すなわち、起こりうる事象の種類が2種類のみの試行を1回だけ実施するのである。
これは二項分布において\(N=1\)とすることと同義である。
\begin{align}
f(x;p)={}_{1}\mathrm{C}_{x}\,p^{x}(1-p)^{1-x}=\frac{1!}{x!(1-x)!}p^{x}(1-p)^{1-x} \label{ベルヌーイ1}\tag{7}
\end{align}
\(N=1\)より、\(x\)および\(1-x\)は0または1となるため、\(x!=1, (1-x)!=1\)となる。
よってこれらを(\ref{ベルヌーイ1})に代入すると
\begin{align}
f(x;p)=\frac{1!}{1\cdot 1}p^{x}(1-p)^{1-x}=p^{x}(1-p)^{1-x}
\end{align}
となる。これがベルヌーイ分布の確率関数である。
ベルヌーイ分布
\begin{gather}
f(x;p)=p^{x}(1-p)^{1-x} \label{ベルヌーイ表式}\tag{8}
\end{gather}
例
コイン(均質でも歪でもよい)を1回だけ振ったとき、「表面が\(x\)回」かつ「裏面が\(1-x\)回」出る確率はベルヌーイ分布に従う。

例題
例題4
面が出る確率がそれぞれ以下で与えられる2つのコインをそれぞれ1回振る試行を考える。
| コイン | 表面が出る確率 | 裏面が出る確率 |
|---|---|---|
| コイン1 | \(\displaystyle{\frac{1}{2}}\) | \(\displaystyle{\frac{1}{2}}\) |
| コイン2 | \(\displaystyle{\frac{1}{4}}\) | \(\displaystyle{\frac{3}{4}}\) |
このとき、コイン1で表面が出る確率、コイン2で裏面が出る確率をそれぞれベルヌーイ分布の確率関数から計算して求め、上の表の値と一致することを確認せよ。
解説
表面が出た回数を\(x\)、表面が出る確率を\(p\)とする。
コイン1について、求める確率を\(f_{1}(x;p)\)とすると(\ref{ベルヌーイ表式})より
\begin{align}
f_{1}(x;p)=\left(\frac{1}{2}\right)^{1}\left(1-\frac{1}{2}\right)^{1-1}= \boxed{ \frac{1}{2}}
\end{align}
となる。
コイン2について、求める確率を\(f_{2}(x;p)\)とすると(\ref{ベルヌーイ表式})より
\begin{align}
f_{2}(x;p)=\left(\frac{1}{4}\right)^{0}\left(1-\frac{1}{4}\right)^{1-0}= \boxed{ \frac{3}{4}}
\end{align}
となる。
4つの離散型確率分布の関係
以上をまとめると下図のようになる。
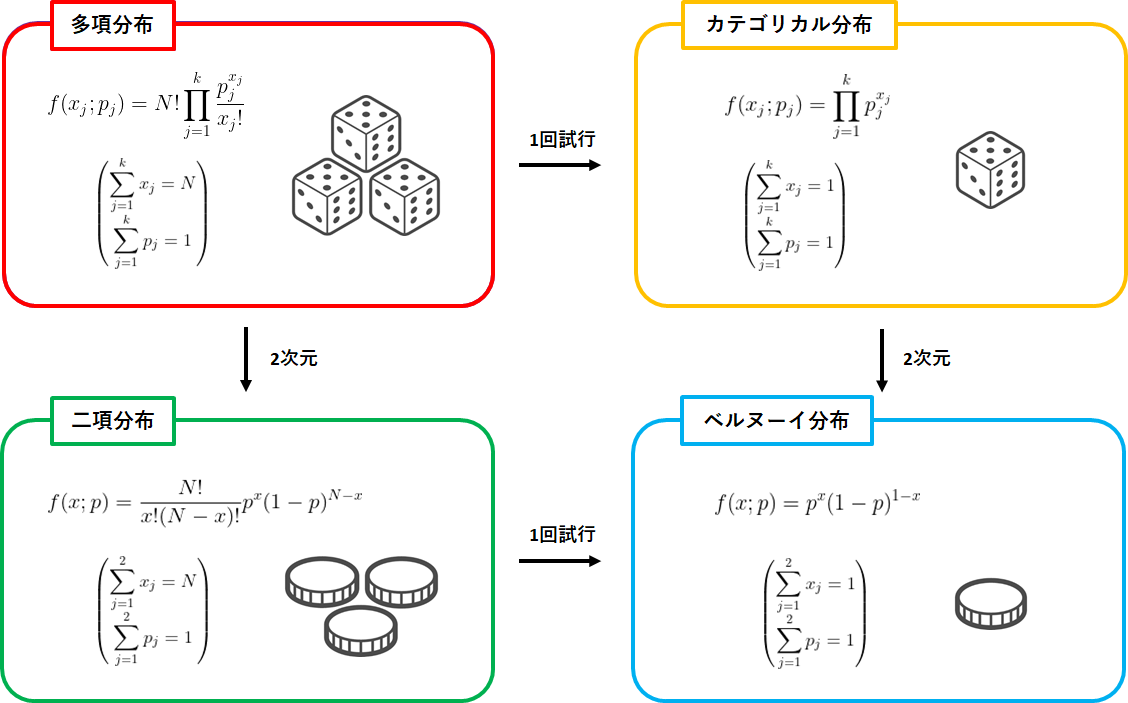
ベルヌーイ分布が最も単純な分布であり、ベルヌーイ分布を三次元以上に拡張したのがカテゴリカル分布、複数回試行に拡張したのが二項分布である。
そしてカテゴリカル分布を複数回試行に、または二項分布を三次元以上に拡張したものが多項分布となる。
いわば多項分布は、ベルヌーイ分布、カテゴリカル分布、二項分布の一般形と言える。
終わりに
離散型確率分布の代表格として他にもポアソン分布があるが、これは上の4つとはまた毛色が違う分布なので別の機会に記事にしようと思う。
やりたいことが多い…
睡眠時間が足りない…
END




コメント
但し書きがあとからでてくるのでわかりにくいです・・・
定理、公式や問題文の最後に「ただし」を添えて条件を加えるのはよくある方法です。
ただ、本記事の場合は単純に私の技量不足かと思います。
申し訳ありません。
もう少しわかりやすい表現、説明の仕方が思いつけば適宜改訂していきます。