【光学】偏光と偏光パラメータ

　光学を扱う上で避けて通れないのが偏光である。

　偏光は実は我々の身近に存在するもの(パソコンやスマホの液晶ディスプレイから発せられる光も偏光)だが、その実態を掴むのは結構難しい。

　特に各偏光の電場の振る舞いをイメージすることが難しく、私も学生時代に苦労した一人だ。

　本記事では、そういったイメージを大事にしながら偏光について解説していく。

　なお、本記事から始まる偏光シリーズでは「光」とは一般的に「可視光」を指すこととする。

偏光とは

　端的に言うと、偏光とは電場と磁場が時間的・空間的に規則性を持って振動する光である。

　どういうこっちゃ、という人もいると思うので基本的なところから解説していく。

　

　まず、光(可視光)とはそもそも電磁波の一種である。

　電磁波とは(特に真空中を伝播する平面波の場合)、次の条件を満たす横波を指す。

　ここで大事なことは、上記3つの条件を満たせば、電場と磁場の振る舞い方に制限が無いことである。

　具体的にデカルト座標系でz方向に進行する光を考えたとき、z方向に垂直な面、すなわちx-y平面内であれば、電場と磁場が面内のある一直線上を振動したり、面内で円を描いたり、何なら軌跡に全く規則性が無くても良いのである。

　これら3つの内、電場と磁場が直線上を振動する、円を描く場合は「規則性を持った」振動であるため、偏光に分類される。

　残りの軌跡に全く規則性が無い場合は、非偏光と呼ばれる。

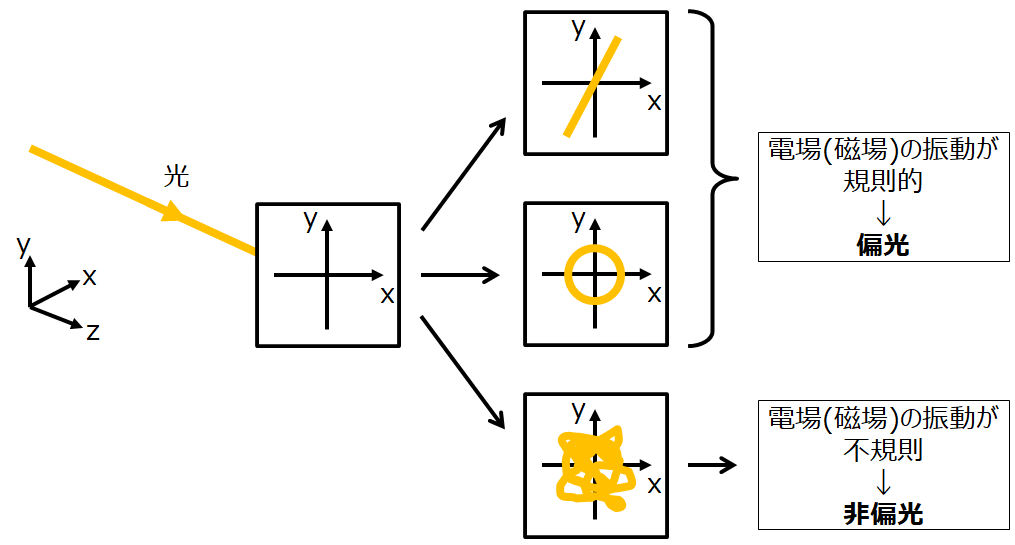
　また偏光は、電場と磁場それぞれが直交する2つの成分に分解できることも特徴である。

　これについては具体的に見た方が分かりやすいので、次節で詳しく取り上げる。

偏光の種類

　ここでは偏光の種類を見ていく。

　ただし電場と磁場の両方を考えると話が冗長になるため、本節以降では電場だけを取り扱うことにする。

　

　デカルト座標系においてz方向に進行する偏光を考える。

　前節でちらっと、偏光では電場は直交する2つの成分に分解できると述べたが、例えば今回はx成分とy成分に分解できたとしよう。

　すなわち、x成分の振幅を\(E_{0x}\)、y成分の振幅を\(E_{0y}\)、位相差を\(\delta\)として電場は次式で表される。

\begin{align}
\vec{E}=(E_{0x}\cos(kz-\omega t),E_{0y}\cos(kz-\omega t+\delta),0)\label{偏光電場}\tag{1}
\end{align}

　ただし位相差は\(0\leq \delta < 2\pi\)の範囲を取り、\(\omega=kc\)である。

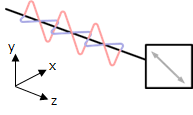
直線偏光

　\(\delta=0,\pi\)となるとき、電場はx-y平面上の直線上を振動する。

　このような偏光を直線偏光と呼ぶ。

一般形

一般的には次のように考えることができる。

　\(\delta=0\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}=(E_{0x}\cos(kz-\omega t),E_{0y}\cos(kz-\omega t),0)
\end{align}

となる。すなわち\(x=E_{0x}\cos(kz-\omega t),y=E_{0y}\cos(kz-\omega t)\)となるため、\(\cos(kz-\omega t)\)を消去してまとめると

\begin{align}
y=\frac{E_{0y}}{E_{0x}}x
\end{align}

となる。つまり電場はx-y平面上において直線\(y=(E_{0y}/E_{0x})x\)上を振動する。

　

　さらに\(\delta=\pi\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}=(E_{0x}\cos(kz-\omega t),E_{0y}\cos(kz-\omega t+\pi),0)=(E_{0x}\cos(kz-\omega t),-E_{0y}\cos(kz-\omega t),0)
\end{align}

となる。すなわち\(x=E_{0x}\cos(kz-\omega t),y=-E_{0y}\cos(kz-\omega t)\)となるため、\(\cos(kz-\omega t)\)を消去してまとめると

\begin{align}
y=-\frac{E_{0y}}{E_{0x}}x
\end{align}

となる。つまり電場はx-y平面上において直線\(y=-(E_{0y}/E_{0x})x\)上を振動する。

例

　例えば\(E_{0x}=0,E_{0y}=E_{0},\delta=0\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}=(0,E_{0y}\cos(kz-\omega t),0)
\end{align}

となる。これはzを固定したx-y平面上においてy軸上を振動する電場を表す。

　

　また\(E_{0x}=E_{0y}=E_{0},\delta=\pi\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}=(E_{0}\cos(kz-\omega t),E_{0}\cos(kz-\omega t+\pi),0)=(E_{0}\cos(kz-\omega t),-E_{0}\cos(kz-\omega t),0)
\end{align}

となる。これはzを固定したx-y平面上において直線\(y=-x\)上を振動する電場を表す。

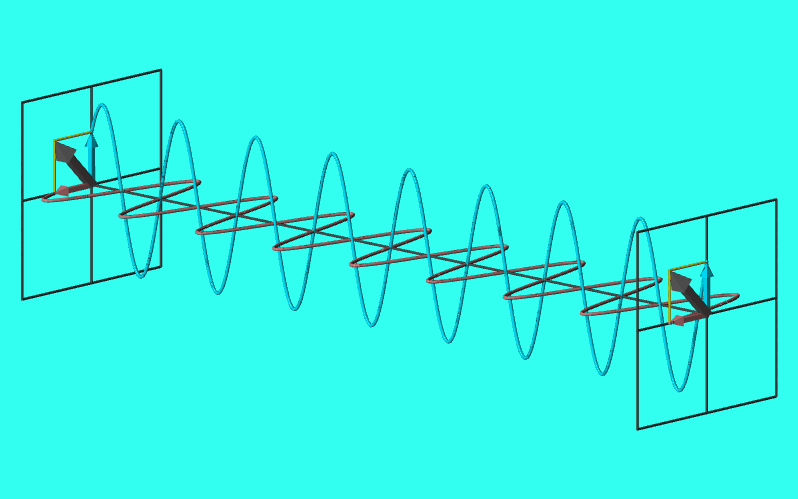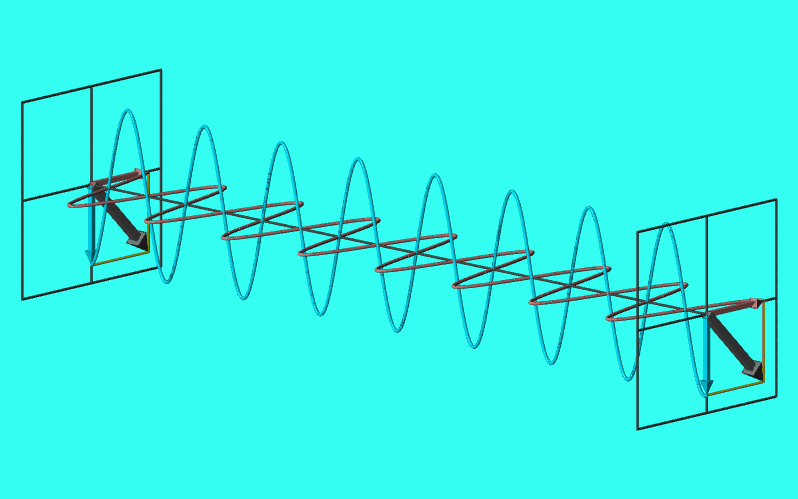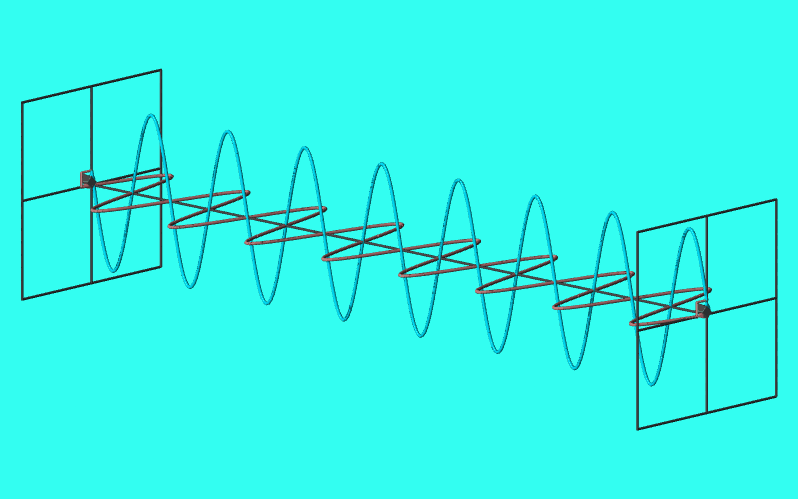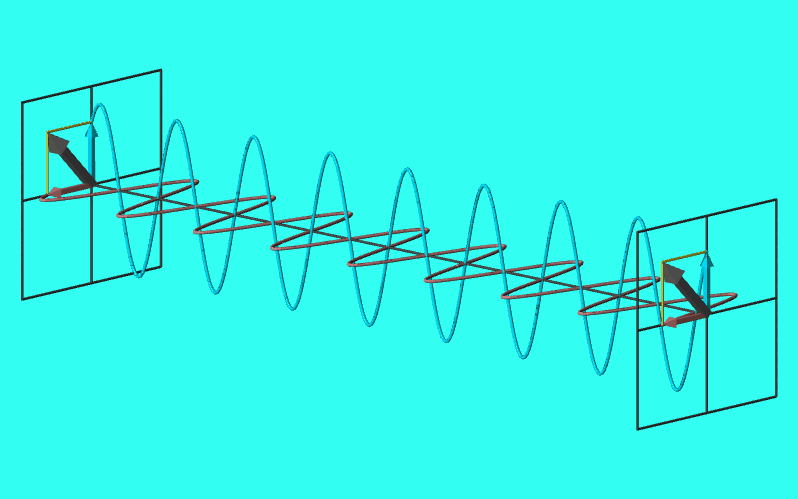
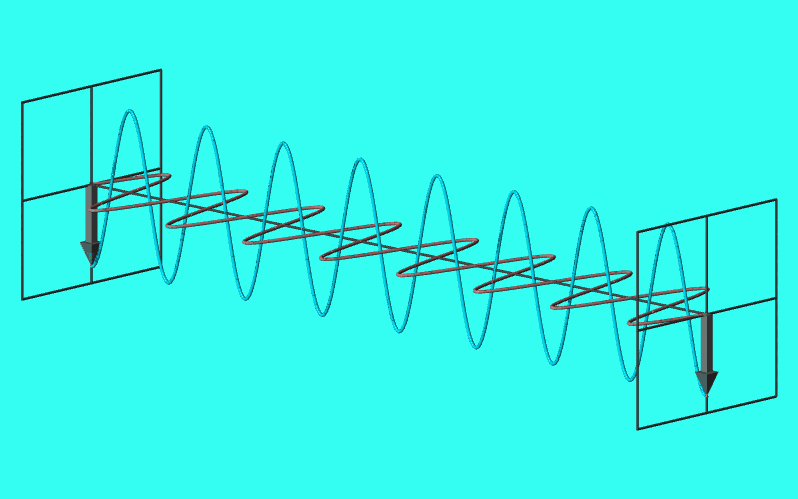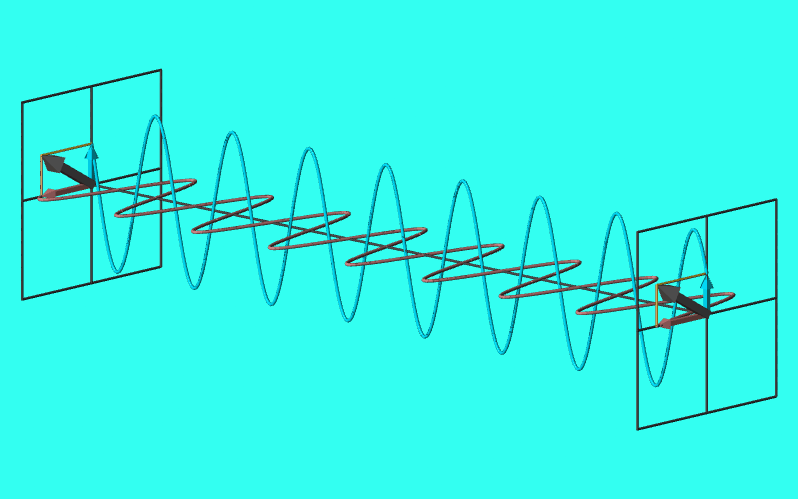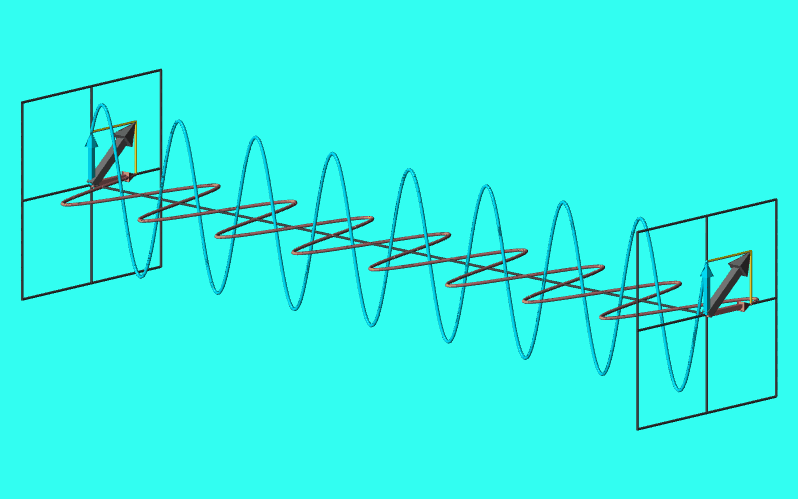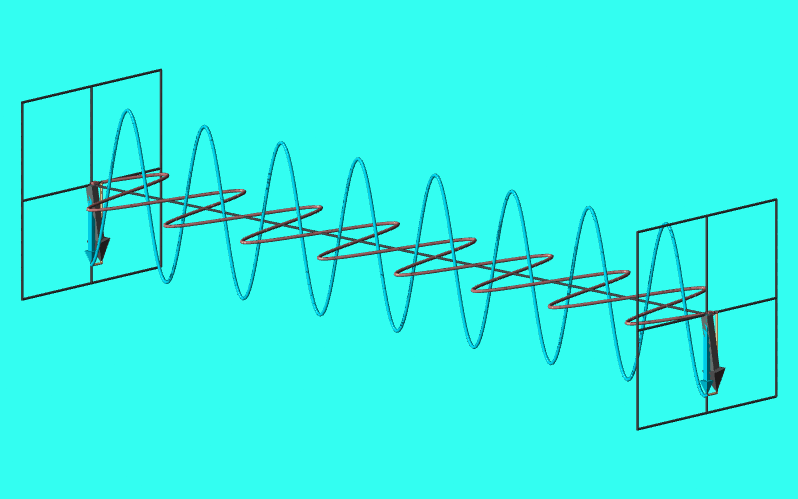
円偏光

　\(E_{0x}=E_{0y}=E_{0},\delta=\pi/2,3\pi/2\)となるとき、電場はx-y平面上で円を描く。

　このような偏光を円偏光と呼ぶ。

　

　一般的には次のように考えることができる。

　\(E_{0x}=E_{0y}=E_{0},\delta=\pi/2\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}=(E_{0}\cos(kz-\omega t),E_{0}\cos(kz-\omega t+\pi/2),0)=(E_{0}\cos(kz-\omega t),-E_{0}\sin(kz-\omega t),0)
\end{align}

となる。すなわち\(x=E_{0}\cos(kz-\omega t),y=-E_{0}\sin(kz-\omega t)\)となるため、それぞれ2乗して足し上げると

\begin{align}
x^{2}+y^{2}=E_{0}^{2} \label{円偏光軌跡}\tag{2}
\end{align}

となる。

　実は\(E_{0x}=E_{0y}=E_{0},\delta=3\pi/2\)のときも(\ref{円偏光軌跡})と同じ結果となり、いずれも電場はx-y平面上で原点を中心とする半径\(E_{0}\)の円を描く。

　両者の違いは何かというと、回転方向が異なる。\(\delta=\pi/2\)のときは時計回り、\(\delta=3\pi/2\)のときは反時計回りとなる。

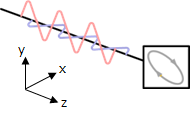
楕円偏光

　上述した直線偏光、円偏光以外の条件では、電場はx-y平面上で楕円を描く。

　このような偏光を楕円偏光と呼ぶ。

一般形

　一般的には次のように考えることができる。

　一般の\(E_{0x},E_{0y},\delta\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}&=(E_{0x}\cos(kz-\omega t),E_{0y}\cos(kz-\omega t+\delta),0)\notag \\
&=\left(E_{0x}\cos(kz-\omega t),E_{0y}\left\{\cos(kz-\omega t)\cos\delta-\sin(kz-\omega t)\sin\delta\right\},0\right)
\end{align}

となる。すなわち\(x=E_{0x}\cos(kz-\omega t),\displaystyle{y=E_{0y}\left\{\cos(kz-\omega t)\cos\delta-\sin(kz-\omega t)\sin\delta\right\}}\)となるため、\(x/E_{0x}=\cos(kz-\omega t),y/E_{0y}=\displaystyle{\cos(kz-\omega t)\cos\delta-\sin(kz-\omega t)\sin\delta}\)として、\(x/E_{0x}\)を\(y/E_{0y}\)に代入して整理すると

\begin{gather}
\frac{y}{E_{0y}}=\frac{x}{E_{0x}}\cos\delta-\sin(kz-\omega t)\sin\delta \notag \\
\frac{y}{E_{0y}}-\frac{x}{E_{0x}}\cos\delta=\sin(kz-\omega t)\sin\delta \notag \\
\left(\frac{y}{E_{0y}}-\frac{x}{E_{0x}}\cos\delta\right)^{2}=\sin^{2}(kz-\omega t)\sin^{2}\delta \notag \\
\left(\frac{y}{E_{0y}}-\frac{x}{E_{0x}}\cos\delta\right)^{2}={1-\cos^{2}(kz-\omega t)}\sin^{2}\delta \notag \\
\left(\frac{y}{E_{0y}}-\frac{x}{E_{0x}}\cos\delta\right)^{2}=\left(1-\frac{x^2}{E_{0x}^2}\right)\sin^{2}\delta \notag \\
\frac{x^2}{E_{0x}^2}-\frac{2xy}{E_{0x}E_{0y}}\cos\delta+\frac{y^2}{E_{0y}^2}=\sin^{2}\delta
\end{gather}

となる。

　一般的に二次曲線\(ax^{2}+bxy+cy^{2}=d\)は、\(b^{2}-4ac<0\)の条件下で楕円となる。

　今回の場合で計算すると

\begin{align}
b^{2}-4ac=\frac{4}{E_{0x}^{2}E_{0y}^{2}}\cos^{2}\delta-4\cdot\frac{1}{E_{0x}^2}\cdot\frac{1}{E_{0y}^2}=\frac{4}{E_{0x}^{2}E_{0y}^{2}}(\cos^{2}\delta-1)=-\frac{4}{E_{0x}^{2}E_{0y}^{2}}\sin^{2}\delta<0
\end{align}

となり、楕円の条件を満たしている。

例

　例えば\(E_{0x}\neq E_{0y},\delta=\pi/2\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}=(E_{0x}\cos(kz-\omega t),E_{0y}\cos(kz-\omega t+\pi/2),0)=(E_{0x}\cos(kz-\omega t),-E_{0y}\sin(kz-\omega t),0)
\end{align}

となる。すなわち\(x=E_{0x}\cos(kz-\omega t),y=-E_{0y}\sin(kz-\omega t)\)となるため、\(x/E_{0x}=\cos(kz-\omega t),y/E_{0y}=-\sin(kz-\omega t)\)として、それぞれ2乗して足し上げると

\begin{align}
\frac{x^{2}}{E_{0x}^{2}}+\frac{y^{2}}{E_{0y}^{2}}=1
\end{align}

となり、電場はx-y平面上で原点を中心とする楕円を描く。

　

　さらに\(E_{0x}=E_{0y}=E_{0},\delta=\pi/6\)のとき、(\ref{偏光電場})は

\begin{align}
\vec{E}&=(E_{0}\cos(kz-\omega t),E_{0}\cos(kz-\omega t+\pi/6),0)\notag \\
&=\left(E_{0}\cos(kz-\omega t),E_{0}\left\{\frac{\sqrt{3}}{2}\cos(kz-\omega t)-\frac{1}{2}\sin(kz-\omega t)\right\},0\right)
\end{align}

となる。すなわち\(x=E_{0}\cos(kz-\omega t),\displaystyle{y=E_{0}\left\{\frac{\sqrt{3}}{2}\cos(kz-\omega t)-\frac{1}{2}\sin(kz-\omega t)\right\}}\)となるため、\(x/E_{0}=\cos(kz-\omega t),y/E_{0}=\displaystyle{\frac{\sqrt{3}}{2}\cos(kz-\omega t)-\frac{1}{2}\sin(kz-\omega t)}\)として、\(x/E_{0}\)を\(y/E_{0}\)に代入して整理すると

\begin{gather}
\frac{y}{E_{0}}=\frac{\sqrt{3}}{2}\cdot \frac{x}{E_{0}}-\frac{1}{2}\sin(kz-\omega t) \notag \\
\frac{y}{E_{0}}-\frac{\sqrt{3}}{2}\cdot \frac{x}{E_{0}}=-\frac{1}{2}\sin(kz-\omega t) \notag \\
\left(\frac{y}{E_{0}}-\frac{\sqrt{3}}{2}\cdot \frac{x}{E_{0}}\right)^{2}=\frac{1}{4}\sin^{2}(kz-\omega t) \notag \\
\left(\frac{y}{E_{0}}-\frac{\sqrt{3}}{2}\cdot \frac{x}{E_{0}}\right)^{2}=\frac{1}{4}{1-\cos^{2}(kz-\omega t)} \notag \\
\left(\frac{y}{E_{0}}-\frac{\sqrt{3}}{2}\cdot \frac{x}{E_{0}}\right)^{2}=\frac{1}{4}\left(1-\frac{x^2}{E_{0}^2}\right) \notag \\
\frac{x^2}{E_{0}^2}-\sqrt{3}\frac{xy}{E_{0}^2}+\frac{y^2}{E_{0}^2}=\frac{1}{4}
\end{gather}
となる。

　一般的に二次曲線\(ax^{2}+bxy+cy^{2}=d\)は、\(b^{2}-4ac<0\)の条件下で楕円となる。

　今回の場合で計算すると

\begin{align}
b^{2}-4ac=\frac{3}{E_{0}^4}-4\cdot\frac{1}{E_{0}^2}\cdot\frac{1}{E_{0}^2}=-\frac{1}{E_{0}^2}<0
\end{align}

となり、楕円の条件を満たしている。

偏光パラメータ

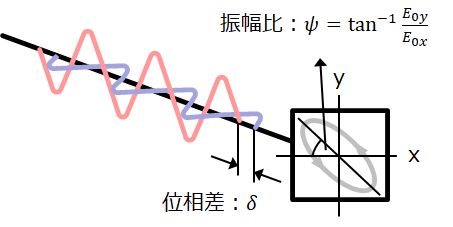
　前節で見てきたように、偏光の種類は2つの直交する電場の振幅\(E_{0x},E_{0y}\)と位相差\(\delta\)で決まる。

　しかし実際の議論では電場の振幅をそのまま使うことはなく、次のパラメータを用いる。

\begin{align}
\psi=\tan^{-1}\frac{E_{0y}}{E_{0x}} \label{振幅比}\tag{3}
\end{align}

　(\ref{振幅比})で定義される\(\psi\)を振幅比角と呼ぶ。

　電場の振幅はともに0以上の値を取るため、\(\psi\)の定義域は\(0\leq \psi \leq \pi/2\)となる。

　(\ref{振幅比})で定義した振幅比角\(\psi\)と位相差\(\delta\)をまとめて偏光パラメータと呼ぶ。

　この2つが決まると、偏光状態(x-y平面上で電場が描く軌跡の種類と電場が動く方向)が決まる。

終わりに

　偏光パラメータが決まれば偏光状態を特定できることがわかったが、\(\psi,\delta\)はいずれも直接測定で求めることは難しい。

　偏光状態の特定においては実際は偏光パラメータではなく、ストークスパラメータと呼ばれる別のパラメータを利用する。

　次の記事でこのストークスパラメータを詳しく取り上げる。

　続きはこちら。