【電子回路】コンパレータ②～ヒステリシスとヒステリシスコンパレータ回路～

　前回

でコンパレータの基本性質を主に見てきた。

　今回はコンパレータ単体ではうまく出力を切り替えられない事例を紹介し、この解決策である「ヒステリシス」について解説していく。

ヒステリシス

　以下のような状況を考えてみよう。

　

　非反転入力端子には5Vの定電圧\(V_{\text{in}+}\)を、反転入力端子には4.99Vの定電圧\(V_{\text{in}-}\)を入力する。

　両者とも理想的な定電圧であれば、\(V_{\text{in}+}>V_{\text{in}-}\)なので、出力電圧は\(V_\text{out(H)}\)で一定になる(図1)。

　しかし、実際の回路では理想的な定電圧は存在せず、ノイズ等の影響で大なり小なり電圧の変動が起こる。

　もし\(V_{\text{in}+}\)と\(V_{\text{in}-}\)ともに\(\pm 0.01\,\text{V}\)の変動幅が存在している場合、\(V_{\text{in}-}\)が\(V_{\text{in}+}\)を上回る、または下回るという挙動が繰り返し発生する。

　すると、出力電圧は\(V_\text{out(H)}\)と\(V_\text{out(L)}\)を行き来する不安定な挙動を起こす(図2)。

　この挙動をチャタリングと呼び、当然このチャタリングは回路動作として不適切である。

　

　ではどうするか？

　実は解決策はそこまで難しくない。

　結論から言うと、\(V_{\text{in}+}\)とは別に、High出力からLow出力に切り替わる際の電圧値\(V_\text{th(H)}\)と、Low出力からHigh出力に切り替わる際の電圧値\(V_\text{th(L)}\)を設ければ良い。

　

　具体的に考えてみよう。

　非反転出力端子に5Vの定電圧\(V_{\text{in}+}\)、反転出力端子にはリニアに時間変化する電圧\(V_{\text{in}-}\)を入力する。

　\(V_{\text{in}-}\)は最初リニアに降下し、5Vを下回った後でリニアに上昇させ、5Vを上回るようにする。

　これまでは\(V_{\text{in}-}\)が5Vを下回ればHigh出力、5Vを上回ればLow出力だった(図3)。

　この切り替わりの基準となる電圧値を別々にする。

　例えば、\(V_{\text{in}-}\)が\(V_\text{th(L)}=4.9\,\text{V}\)を下回ったらHigh出力、\(V_{\text{in}-}\)が\(V_\text{th(H)}=5.1\,\text{V}\)を上回ったらLow出力となるようにするのである(図4)。

　

　こうすれば、\(V_{\text{in}-}\)が\(V_\text{th(L)}\)付近の定電圧でも一度\(V_\text{th(L)}\)を下回れば\(V_\text{out}\)はHigh出力で固定される(図5)。

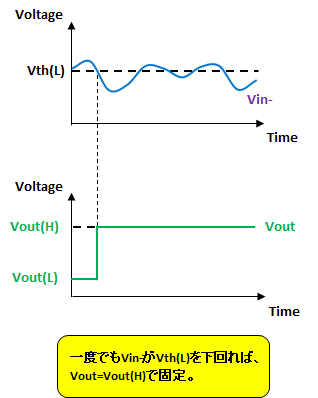
　また、\(V_{\text{in}-}\)が\(V_\text{th(H)}\)付近の定電圧でも一度\(V_\text{th(H)}\)を上回れば\(V_\text{out}\)はLow出力で固定される(図6)。

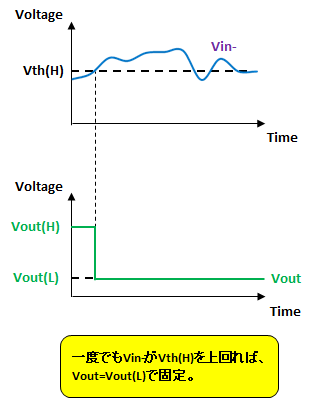
　これら\(V_\text{th(H)},V_\text{th(L)}\)を閾値電圧と呼び、閾値電圧を持たせることを「ヒステリシスを設ける」という。

　そして閾値電圧の差\(\Delta V_\text{th}=V_\text{th(H)}-V_\text{th(L)}\)をヒステリシス幅と呼ぶ。

ヒステリシスコンパレータ回路

　ではここで具体的に、コンパレータにヒステリシスを設ける回路を見ていく。

　いくつか種類があるが、最もオーソドックスな回路を図7に示す。

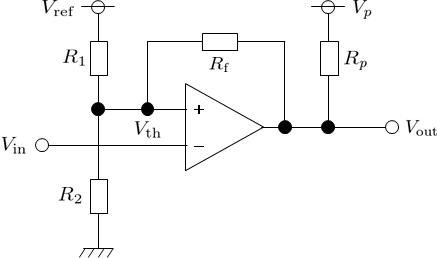
　ただし、コンパレータはオープンコレクタ出力方式とする。

　図7の回路では\(V_\text{out}\)の値に応じて、非反転入力端子の入力電圧\(V_\text{th}\)が異なる値を取る。

　

　まず出力がLow、すなわち\(V_\text{out}=V_\text{out(L)}\)となる場合を考える。

　このとき、コンパレータの出力は接地されているため、\(V_\text{out}=V_\text{out}(L)=0\,\text{V}\)となる。

　よってLow出力時は図8のように、3つの抵抗から成る回路と等価となる。

　よってキルヒホッフの法則より

\begin{align}
\frac{V_{\text{ref}}-V_{\text{th(L)}}}{R_{1}}=\frac{V_{\text{th(L)}}}{R_{\text{f}}}+\frac{V_{\text{th(L)}}}{R_{\text{2}}}
\end{align}

となる。

　これを\(V_{\text{th(L)}}\)について解けば

\begin{align}
\boxed{V_{\text{th(L)}}=\frac{V_{\text{ref}}}{R_{1}}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{f}}}\right)^{-1}}
\end{align}

となる。

　

　続いて出力がHigh、すなわち\(V_\text{out}=V_\text{out(H)}\)となる場合を考える。

　このとき、コンパレータの出力はオープンになっているため、\(V_\text{p}\)からの電流は抵抗\(R_\text{f}\)へと流れる。

　よってHigh出力時は図9のように、4つの抵抗から成る回路と等価となる。

　よってキルヒホッフの法則より

\begin{align}
\frac{V_{\text{p}}-V_{\text{th(H)}}}{R_{\text{p}}+R_{\text{f}}}+\frac{V_{\text{ref}}-V_{\text{th(H)}}}{R_{1}}=\frac{V_{\text{th(H)}}}{R_{2}}
\end{align}

となる。

　これを\(V_{\text{th(H)}}\)について解けば

\begin{align}
\boxed{V_{\text{th(H)}}=\left(\frac{V_{\text{p}}}{R_{\text{p}}+R_{\text{f}}}+\frac{V_{\text{ref}}}{R_{1}}\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{p}}+R_{\text{f}}}\right)^{-1}}
\end{align}

となる。

　

　よってヒステリシス幅\(\Delta V_{\text{th}}=V_{\text{th(H)}}-V_{\text{th(L)}}\)は

\begin{align}
\Delta V_{\text{th}}=\left(\frac{V_{\text{p}}}{R_{\text{p}}+R_{\text{f}}}+\frac{V_{\text{ref}}}{R_{1}}\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{p}}+R_{\text{f}}}\right)^{-1}-\frac{V_{\text{ref}}}{R_{1}}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{f}}}\right)^{-1}
\end{align}

と求められる。

　この結果を見ると、ヒステリシス幅は基準電圧\(V_\text{ref}\)に依存することがわかる。

　そしてこの基準電圧の依存度は、抵抗値で操作することが可能だ。

　具体的には\(R_{\text{f}}\gg R_{\text{p}}\)として\(R_{\text{f}}+R_{\text{p}}\simeq R_{\text{f}}\)とみなせるようにする。

　このとき

\begin{align}
\Delta V_{\text{th}}&\simeq \left(\frac{V_{\text{p}}}{R_{\text{f}}}+\frac{V_{\text{ref}}}{R_{1}}\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{f}}}\right)^{-1}-\frac{V_{\text{ref}}}{R_{1}}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{f}}}\right)^{-1}\notag \\
&=\frac{V_{\text{p}}}{R_{\text{f}}}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{f}}}\right)^{-1} \notag \\
&\boxed{\Delta V_{\text{th}}\simeq \frac{V_{\text{p}}}{R_{\text{f}}}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{f}}}\right)^{-1}}
\end{align}

となり、基準電圧\(V_{\text{ref}}\)の依存が無視できるようになる。

　

　ちなみに\(V_\text{out}=V_\text{out(H)}\)にも着目するとキルヒホッフの法則より

\begin{align}
\frac{V_{\text{p}}-V_{\text{out(H)}}}{R_{\text{p}}}=\frac{V_{\text{out(H)}}-V_{\text{th(H)}}}{R_{\text{f}}}
\end{align}

となるため、これを整理すると

\begin{align}
\boxed{V_{\text{out(H)}}=\frac{R_{\text{f}}V_{\text{p}}+R_{\text{p}}V_{\text{th(H)}}}{R_{\text{f}}+R_{\text{p}}}}
\end{align}

となる。

　よって\(R_{\text{f}}\gg R_{\text{p}}\)のとき

\begin{align}
\boxed{V_{\text{out(H)}}\simeq V_{\text{p}}}
\end{align}

となって出力がプルアップ電圧とほぼ同値となる。

LTspiceによるシミュレーション

　ここで、実際にLTspiceでヒステリシスコンパレータ回路を動作させたシミュレーション結果を図10に示す。

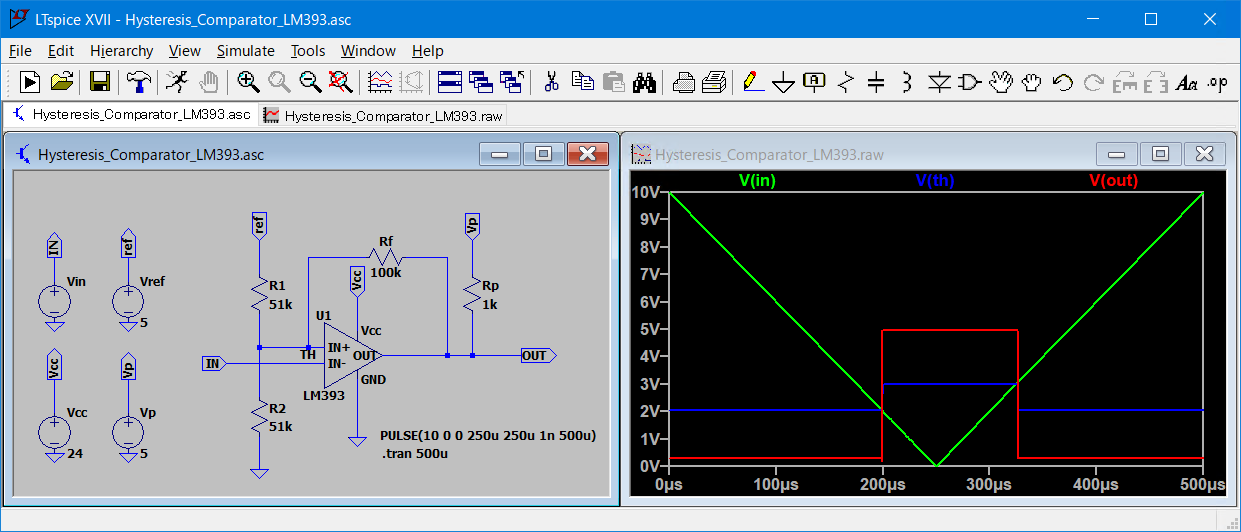
　本回路ではプルアップ抵抗\(R_\text{p}\)に対して100倍の抵抗を\(R_\text{f}\)にあてている。

　このとき、Low出力時の閾値電圧\(V_\text{th(L)}\)は

\begin{align}
V_\text{th(L)}&=\frac{V_\text{ref}}{R_1}\left(\frac{1}{R_1} +\frac{1}{R_2} +\frac{1}{R_\text{f}}\right)^{-1}\notag \\
&=\frac{5\,\text{V}}{51\,\text{k}\Omega}\left(\frac{1}{51\,\text{k}\Omega}+\frac{1}{51\,\text{k}\Omega}+\frac{1}{100\,\text{k}\Omega}\right)^{-1}\notag \\
&=1.992\,\text{V}\simeq 2\,\text{V}
\end{align}

であり、High出力時の閾値電圧\(V_\text{th(H)}\)は

\begin{align}
V_\text{th(H)}&=\left(\frac{V_{\text{p}}}{R_{\text{p}}+R_{\text{f}}}+\frac{V_{\text{ref}}}{R_{1}}\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{\text{p}}+R_{\text{f}}}\right)^{-1} \notag \\
&=\left(\frac{5\,\text{V}}{51\,\text{k}\Omega}+\frac{5\,\text{V}}{100\,\text{k}\Omega+1\,\text{k}\Omega}\right) \left(\frac{1}{51\,\text{k}\Omega}+\frac{1}{51\,\text{k}\Omega}+\frac{1}{100\,\text{k}\Omega+1\,\text{k}\Omega}\right)^{-1}\notag \\
&=3.004\,\text{V}\simeq 3\,\text{V}
\end{align}

である。

　さらに\(R_\text{f}\gg R_\text{p}\)として、\(R_\text{f}+R_\text{p}\simeq R_\text{f}\)の近似を適用すると、

\begin{align}
V_\text{th(H)}&=\left(\frac{V_\text{ref}}{R_1}+\frac{V_\text{p}}{R_\text{f}}\right)\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_\text{f}} \right)^{-1} \notag \\
&=\left(\frac{5\,\text{V}}{51\,\text{k}\Omega}+\frac{5\,\text{V}}{100\,\text{k}\Omega}\right)\left(\frac{1}{51\,\text{k}\Omega}+\frac{1}{51\,\text{k}\Omega}+\frac{1}{100\,\text{k}\Omega}\right)^{-1}\notag \\
&=3.007\,\text{V}\simeq 3\,\text{V}
\end{align}

となり、小数点以下第3位以降の精度を要求しないなら適切な近似となる。

　よって本回路ではヒステリシス幅は入力電圧に関係なく

\begin{align}
\Delta V_\text{th}=V_\text{th(H)}-V_\text{th(L)}=1\,\text{V}
\end{align}

となる。

　

　またHigh出力時の出力電圧\(V_\text{out}=V_\text{out(H)}\)は

\begin{align}
V_{\text{out(H)}}&=\frac{R_{\text{f}}V_{\text{p}}+R_{\text{p}}V_{\text{th(H)}}}{R_{\text{f}}+R_{\text{p}}} \notag \\
&=\frac{100\,\text{k}\Omega \times 5\,\text{V}+1\,\text{k}\Omega\times 3\,\text{V}}{100\,\text{k}\Omega+1\,\text{k}\Omega} \notag \\
&=4.98\,\text{V}\simeq 5\,\text{V}
\end{align}

となり、プルアップ電圧\(V_\text{p}\)とほぼ同値である。

　これはシミュレーション結果(赤線)からも確認できる。

終わりに

　ヒステリシスコンパレータ回路には他にも種類があるが、今後扱う必要性が生じた際にまとめて記事にしようと思う。

　ようやく回路設計らしい業務を開始できたので、初心者の内にできる範囲で習得できたことを言語化したいが、どこまでできるか…

　

　END