物理をする上で必須となる数学の内の1つが「ベクトル解析」だ。
座標の各点に量と向き(要はベクトル)を与える「ベクトル場」なるものが登場し、主にその微分と積分を扱う単元になる。
ベクトルの微分がいわゆるグラディエント(\(\text{grad}\),勾配)、ダイバージェンス(\(\text{div}\),発散)、ローテーション(\(\text{rot}\),回転)であり、これらは計算自体は難しいものではないため覚えやすい。
しかし厄介なのが積分、すなわち線積分と面積分だ。
両者とも電磁気学では必須の数学なのだが、一般的な関数に対する積分とは計算の仕方が結構異なり、注意が必要になる部分も多い。
私自身、両者とも計算方法をすぐに忘れることが多く、電磁気学の復習時もかなり苦労した。
そこで今回からは私自身の備忘録も兼ねて、線積分と面積分の計算法と例題をまとめ、記事にしていこうと思う。
まずは線積分から見ていく。
概要
線積分では「線」と書かれている通り、ある座標系に線を引き、その線に沿って積分を実行する。
その線では直線でも曲線でも良いし、開いていても閉じていても良い。
しかし、積分されるものが関数ではなくベクトル場であることが、これまでの積分との大きな違いだ。
例えばベクトル場\(\vec{A}\)があったとき、これを経路\(C\)に沿って線積分する場合は
\begin{align}
\int_{C}\vec{A}\cdot d\vec{r}
\end{align}
を計算する。
ただし\(d\vec{r}\)は経路\(C\)を細かく分割した微小ベクトルであり、線素ベクトルと呼ばれる。
線積分の基本的な計算の手順は下記のようになる。
(1) 経路\(C\)上の位置ベクトル\(\vec{r}\)を1つの変数で表す(パラメーター表示する)。ここではその変数を\(t\)とする。
(2) (1)で得た位置ベクトル\(\vec{r}\)を変数\(t\)で微分し、その上で\(t\)の微小量\(dt\)をかける(積分変数の変数変換をする)。これが線素ベクトル\(d\vec{r}\)となる。
\begin{align}
d\vec{r}=dt\frac{d}{dt}\vec{r}
\end{align}
(3) (1)での経路\(C\)の位置ベクトル\(\vec{r}\)を線積分するベクトル場\(\vec{A}\)に適用する。
(4) (2)で得た線素ベクトル\(d\vec{r}\)と、(3)でパラメーター表示を適用したベクトル場\(\vec{A}\)の内積を計算する。
(5) 経路\(C\)上での\(t\)の変化を積分範囲とし、(4)で得た内積を積分する。
経路\(C\)が複雑な場合は、経路上の位置ベクトル\(\vec{r}\)を1つの変数で表せられるまで単純な経路に分割し、各経路について上記の計算を実施して、最後にそれらを足し上げればよい。
これだけではまだイメージがつかないだろうから、実際に例題を解いていこう。
例題1
例題1
\(a\)を定数として\(\vec{A}=(-ay,ax,0)\)というベクトル場を考える。このとき、次の問に答えよ。
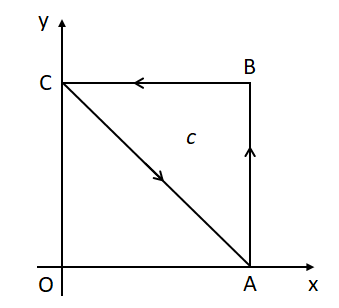
(1) 図1のように点A:\((1,0,0)\)、点B:\((1,1,0)\)、点C:\((0,1,0)\)の3点をつないだ閉曲線\(c\)を考える。この閉曲線\(c\)に沿った\(\vec{A}\)の線積分を求めよ。ただし線積分の向きは図1の矢印の方向(反時計方向)を正にとる。
(2) 図2のように点A:\((1,0,0)\)から点C:\((0,1,0)\)まで、原点Oを中心とする半径1の円の円周に沿って曲線\(\ell\)を引く。この曲線\(\ell\)に沿った\(\vec{A}\)の線積分を求めよ。ただし線積分の向きは図2の矢印の方向(反時計方向)を正にとる。

解説
(1)
まずは経路\(c\)上の位置ベクトル\(\vec{r}\)を1つの変数で表す。
積分経路\(c\)は3本の線分から構成されているため、各線分の線積分を計算して足し上げることにする。
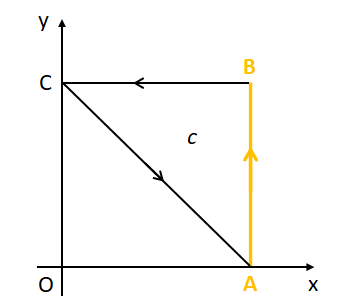
(i) 線分AB上での線積分
線分AB上の位置ベクトルを\(\vec{r}_{1}\)とすると、
\begin{align}
\vec{r}_{1}=(1,t,0) \tag{1}
\end{align}
となるため、線素ベクトル\(d\vec{r}_{1}\)は
\begin{align}
d\vec{r}_{1}=dt\frac{d}{dt}\vec{r}_{1}=dt(0,1,0) \tag{2}\label{sensekirei1-1-1}
\end{align}
となる。
さらにベクトル場\(\vec{A}\)に位置ベクトル\(\vec{r}_{1}\)を適用すると
\begin{align}
\vec{A}=(-at,a,0) \tag{3}\label{sensekirei1-1-2}
\end{align}
となる。
よって経路の矢印の向きを考慮すると積分範囲は\(t:0\to 1\)となるため、線分AB上での線積分は(\ref{sensekirei1-1-1})と(\ref{sensekirei1-1-2})より
\begin{align}
\int_{\text{AB}}\vec{A}\cdot d\vec{r}_{1}=\int_{0}^{1}(-at,a,0)\cdot dt(0,1,0)=a\int_{0}^{1}dt=a \tag{4}
\end{align}
となる。
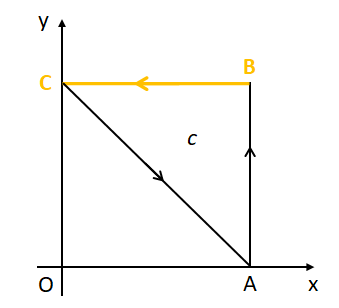
(ii)線分BC上での線積分
線分BC上での位置ベクトルを\(\vec{r}_{2}\)とすると、
\begin{align}
\vec{r}_{2}=(t,1,0) \tag{5}
\end{align}
となるため、線素ベクトル\(d\vec{r}_{2}\)は
\begin{align}
d\vec{r}_{2}=dt\frac{d}{dt}\vec{r}_{2}=dt(1,0,0) \tag{6}\label{sensekirei1-2-1}
\end{align}
となる。
さらにベクトル場\(\vec{A}\)に位置ベクトル\(\vec{r}_{2}\)を適用すると
\begin{align}
\vec{A}=(-a,at,0) \tag{7}\label{sensekirei1-2-2}
\end{align}
となる。
よって経路の矢印の向きを考慮すると積分範囲は\(t:1\to 0\)となるため、線分BC上での線積分は(\ref{sensekirei1-2-1})と(\ref{sensekirei1-2-2})より
\begin{align}
\int_{\text{BC}}\vec{A}\cdot d\vec{r}_{2}=\int_{1}^{0}(-a,at,0)\cdot dt(1,0,0)=-a\int_{1}^{0}dt=a \tag{8}
\end{align}
となる。
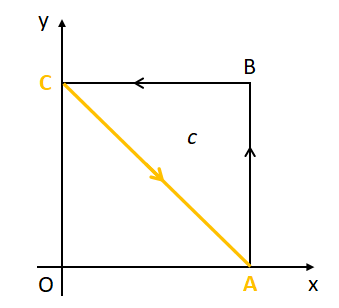
(iii)線分CA上での線積分
線分CA上での位置ベクトルを\(\vec{r}_{3}\)とすると、
\begin{align}
\vec{r}_{3}=(t,-t+1,0) \tag{9}
\end{align}
となるため、線素ベクトル\(d\vec{r}_{3}\)は
\begin{align}
d\vec{r}_{3}=dt\frac{d}{dt}\vec{r}_{3}=dt(1,-1,0) \tag{10}\label{sensekirei1-3-1}
\end{align}
となる。
さらにベクトル場\(\vec{A}\)に位置ベクトル\(\vec{r}_{3}\)を適用すると
\begin{align}
\vec{A}=(-a(-t+1),at,0)=(a(t-1),at,0) \tag{11}\label{sensekirei1-3-2}
\end{align}
となる。
よって経路の矢印の向きを考慮すると積分範囲は$\(t:0\to 1\)となるため、線分CA上での線積分は(\ref{sensekirei1-3-1})と(\ref{sensekirei1-3-2})より
\begin{align}
\int_{\text{CA}}\vec{A}\cdot d\vec{r}_{3}&=\int_{0}^{1}(a(t-1),at,0)\cdot dt(1,-1,0) \notag \\
&=\int_{0}^{1}\{a(t-1)-at\}dt \notag \\
&=-a\int_{0}^{1}dt=-a \tag{12}
\end{align}
となる。
以上より、求める線積分は(i)~(iii)より
\begin{align}
\int_{c}\vec{A}\cdot d\vec{r}=a+a-a=\boxed{a} \tag{13}
\end{align}
となる。
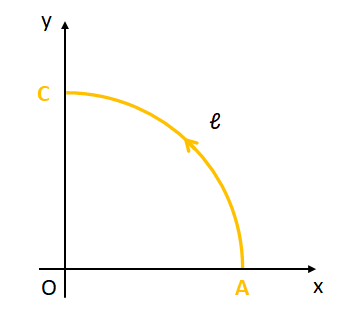
(2)
曲線\(\ell\)は原点Oを中心とする半径1の円の一部であるため、その位置ベクトルを\(\vec{r}\)とすると極座標表示を用いて
\begin{align}
\vec{r}=(\cos\theta,\sin\theta,0) \tag{14}
\end{align}
となる。
よって線素ベクトル\(d\vec{r}\)は
\begin{align}
d\vec{r}=d\theta\frac{d}{d\theta}\vec{r}=d\theta(-\sin\theta,\cos\theta,0) \tag{15}\label{sensekirei1-4-1}
\end{align}
となる。
さらにベクトル場\(\vec{A}\)に位置ベクトル\(\vec{r}\)を適用すると
\begin{align}
\vec{A}=(-a\sin\theta,a\cos\theta,0) \tag{16}\label{sensekirei1-4-2}
\end{align}
となる。
よって経路の矢印の向きを考慮すると積分範囲は\(\theta:0\to \pi/2\)となるため、曲線\(\ell\)上での線積分は(\ref{sensekirei1-4-1})と(\ref{sensekirei1-4-2})より
\begin{align}
\int_{\ell}\vec{A}\cdot d\vec{r}&=\int_{0}^{\pi/2}(-a\sin\theta,a\cos\theta,0)\cdot d\theta(-\sin\theta,\cos\theta,0) \notag \\
&=\int_{0}^{\pi/2}a(\sin^{2}\theta+\cos^{2}\theta)d\theta \notag \\
&=a\int_{0}^{\pi/2}d\theta=\boxed{\frac{\pi a}{2}}\tag{17}
\end{align}
となる。
例題2
例題2
ベクトル場\(\vec{A}=a(x^{2}z,-xy^{3}z^{2},xy^{2}z)\)があるとき、原点O:\((0,0,0)\)と点P:\((1,1,1)\)を結ぶ線分OP上でのベクトル場\(\vec{A}\)の線積分を求めよ。
ただし線積分の向きは原点Oから点Pへ向かう方向を正にとる。
解説
まずは線分OP上の位置ベクトル\(\vec{r}\)を1つの変数で表す。
線分OPの位置ベクトルを\(\vec{r}\)とすると、
\begin{align}
\vec{r}=(t,t,t) \tag{18}
\end{align}
となるため、線素ベクトル\(d\vec{r}\)は
\begin{align}
d\vec{r}=dt\frac{d}{dt}\vec{r}=dt(1,1,1) \tag{19}\label{sensekirei2-1}
\end{align}
となる。
さらにベクトル場\(\vec{A}\)に位置ベクトル\(\vec{r}\)を適用すると
\begin{align}
\vec{A}=a(t^{3},-t^{6},t^{4}) \tag{20}\label{sensekirei2-2}
\end{align}
となる。
よって経路の向きを考慮すると積分範囲は\(t:0\to 1\)となるため、線分OP上での線積分は(\ref{sensekirei2-1})と(\ref{sensekirei2-2})より
\begin{align}
\int_{\ell}\vec{A}\cdot d\vec{r}&=\int_{0}^{1}a(t^{3},-t^{6},t^{4})\cdot dt(1,1,1) \notag \\
&=\int_{0}^{1}a(-t^{6}+t^{4}+t^{3})dt \notag \\
&=a\left[-\frac{t^{7}}{7}+\frac{t^{5}}{5}+\frac{t^{4}}{4}\right] \notag \\
&=a\left(-\frac{1}{7}+\frac{1}{5}+\frac{1}{4}\right)=\boxed{\frac{43}{140}a} \tag{21}
\end{align}
となる。
終わりに
線積分に関してはここで締める。
線積分する経路をパラメーター表示した上で線素ベクトルを求めることが出来れば、そこまでハードルは高くないと思う。
次回は面積分を取り扱う予定だ。
END




コメント
有難うございます。大変参考になりました。一部、。初歩的な記載ミスが有ったのでお知らせします。第1問で、dr2=dtdr2/dtがr1になっています。また、dr3でも同様な誤りが有ります。私の様な数学が不得意な人間は、そこでつまずいてしまいますので、訂正をお願いします。私は73歳で化学出身で、現役時代は出光の中央研究所にいました。昔から化学よりも数学が好きでコツコツやっていました。量子力学の初歩は学んだので、今は相対性理論に挑戦しています。渡邊隆佐
ryusuke15843@nifty.com
誤植部分を訂正致しました。
ご指摘ありがとうございます。
大変助かります。
現在大学にて物理に苦戦している1年生です。仕事の理解に悩んでいたのですが、こちらのページが大変参考になりました。ありがとうございました。
コメントありがとうございます。
お役に立てたようで良かったです。