【AI】機械学習 by Python：分類編①～実装例と概説～

　機械学習に手を出しましたということで、最初に回帰分析の実装例の解説をしてきた。

　今回は同じ要領で、教師あり学習の1つである「分類」についてみていく。

実装例

　実際に、Pythonで分類のプログラムを実装した場合にどうなるか。
　下に例を示す。

# モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.colors import ListedColormap
import sklearn
from sklearn.linear_model import LogisticRegression
from sklearn import metrics

# データセットのインポート
file=pd.read_csv('logistic.csv',header=None)

# データの割り振り
X=file.iloc[:,0:2]
Y=file.iloc[:,2]

# データセットを学習データ（8割）とテストデータ（2割）に分割（random_stateは0）
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)
# 分割の確認
print('分割の確認：',X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)

# 学習実行
# インスタンスの作成
model=LogisticRegression()
# モデルの作成
model.fit(X_train,Y_train)

# 直線の確認
# 切片
print('切片の値 = ', model.intercept_)
# 係数
print('係数の値 = ', model.coef_)

# 学習データからの予測値
pred_train = model.predict(X_train)
# テストデータからの予測値
pred_test = model.predict(X_test)

# 学習データを用いた分類モデルの評価
print('正解率(学習データ) = ', metrics.accuracy_score(Y_train, pred_train))
print('適合率(学習データ) = ', metrics.precision_score(Y_train, pred_train))
print('再現率(学習データ) = ', metrics.recall_score(Y_train, pred_train))
print('F値(学習データ) = ', metrics.f1_score(Y_train, pred_train))

# テストデータを用いた分類モデルの評価
print('正解率(テストデータ) = ', metrics.accuracy_score(Y_test, pred_test))
print('適合率(テストデータ) = ', metrics.precision_score(Y_test, pred_test))
print('再現率(テストデータ) = ', metrics.recall_score(Y_test, pred_test))
print('F値(テストデータ) = ', metrics.f1_score(Y_test, pred_test))

# データセットおよび直線の図示
plt.figure(figsize=(4,4))
plt.scatter(file.iloc[:,0], file.iloc[:,1],c=file.iloc[:,2], cmap=ListedColormap(['#FF0000', '#0000FF']))
plt.plot(file.iloc[:,0], -file.iloc[:,0]*model.coef_[0,0]/model.coef_[0,1]-model.intercept_[0]/model.coef_[0,1])
plt.show()

　ただし、「#」以降の記述はコメントであり、プログラムに直接影響はしない。

　上記プログラムを実行すると、例えば次のような結果が出力される。

分割の確認： (160, 2) (40, 2) (160,) (40,)
切片の値 =  [-9.71024304]
係数の値 =  [[0.04871103 1.89741032]]
正解率(学習データ) =  0.91875
適合率(学習データ) =  0.9195402298850575
再現率(学習データ) =  0.9302325581395349
F値(学習データ) =  0.9248554913294798
正解率(テストデータ) =  0.875
適合率(テストデータ) =  0.8125
再現率(テストデータ) =  0.8666666666666667
F値(テストデータ) =  0.8387096774193549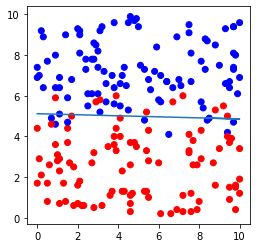

　

　上記プログラムは何をしているかというと、

といったことをしている。

　

　実際にプログラムを実行したい場合は、下記ボタンよりcsvファイル「logistic.csv」をダウンロードしてプログラムの保存先に保存すること。

分類概説

　分類とは上で見てきたように、データ群をいくつかのカテゴリーに分けることである。

　分類には大きく、2つのカテゴリーに分ける「二項分類」と、3つ以上のカテゴリーに分ける「多項分類」の2種類が存在する。

　

　上で見てきた例は、線形分離可能な二項分類の問題をロジスティック回帰を利用して解いている。

　ロジスティック回帰とは「回帰」という言葉がついているが、立派な分類問題を解くためのアルゴリズムの1つであり、線形分離可能な(直線でカテゴリーを分割できる)二項分類の問題に用いられる。

　アルゴリズムの詳細を知らなくてもプログラムの実装はできるので、ここでは深く掘り下げることはしない。
　気が向いたら別記事に詳細を書こうと思う。

次回予告

　次回から前の回帰分析と同様に、上で示したプログラムのコード一文一文を詳しく見ていく。

　それぞれのコードが何を意味し、何の役割を果たしているのか、自分の勉強も兼ねながらまとめていくつもりだ。

　

　END

　

　※追記
　プログラムの詳説記事の執筆開始。