解析的に解けない微分方程式を解く際には数値計算を利用する。
しかし微分方程式を数値計算で解くには、従来では微分方程式の数値計算手法の理解が必要であり、プログラムを組む際の大きなハードルとなっていた。
しかし、PythonのSciPyパッケージのodeintモジュールを使うと、誤解を恐れず言えばたとえ計算手法が良く分かっていなくても微分方程式数値計算のプログラムを構築できる。
対象は1階の常微分方程式のみだが、それでも十分強力だ。
本記事では実際にodeintモジュールを利用した常微分方程式の数値計算プログラム例を取り上げていく。
例1:空気抵抗を含む斜方投射
まずは典型的な力学の問題である、空気抵抗を含む斜方投射をodeintモジュールで解いてみる。
当然解くべき微分方程式は運動方程式であり、具体的には下式になる。
\begin{align}
\begin{cases}
\displaystyle{m\frac{d^{2}x}{dt^{2}}=-\mu\frac{dx}{dt}} \\ \\
\displaystyle{m\frac{d^{2}y}{dt^{2}}=-\mu\frac{dy}{dt}-mg}
\end{cases}\tag{1}\label{rei1-1}
\end{align}
運動方程式は時間の2階微分を含むが、高階の常微分方程式は1階の連立常微分方程式で置き換えられるため、odeintモジュールで扱うことができる。
下記、プログラムの実装例を示す。
%matplotlib notebook
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
#運動方程式
#var[0]=x,var[1]=y,var[2]=vx,var[3]=vy
def eom(var, t, m, g, mu):
dxdt = var[2]
dydt = var[3]
dvxdt = -(mu*var[2]/m)
dvydt = -g-(mu*var[3]/m)
return [dxdt, dydt, dvxdt, dvydt]
#2dグラフ
def plot2d(t_list, var_list):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlabel("$x[m]$")
ax.set_ylabel("$y[m]$")
ax.plot(var_list[:, 0], var_list[:, 1])
ax.set_aspect('equal')
plt.show()
#メイン
if (__name__ == '__main__'):
t_list = np.linspace(0.0, 10, 500)
m = 0.1 #質点の質量[kg]
g = 9.8 #重力加速度[m^2/s]
mu = 1*10**(-3) #抵抗係数[N・s/m]
var_init = [0, 300, 20, 20] #初期値
var_list = odeint(eom, var_init, t_list, args = (m, g, mu))
#グラフ表示
plot2d(t_list, var_list)上記プログラムを実行すると、下図のような質点の運動の軌跡が出力される。
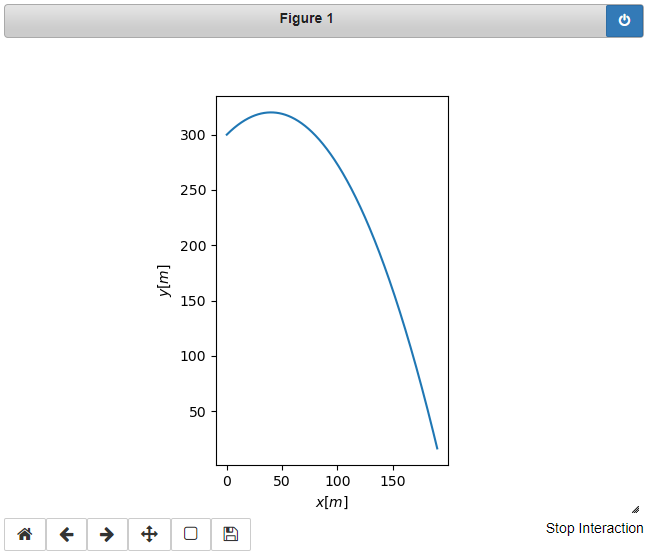
コードの詳細を見ていく。
まず
%matplotlib notebookでJupyter Notebook内にグラフを表示できるようにする。
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as pltはモジュールのインポート。
def eom(var, t, m, g, mu):
dxdt = var[2]
dydt = var[3]
dvxdt = -(mu*var[2]/m)
dvydt = -g-(mu*var[3]/m)
return [dxdt, dydt, dvxdt, dvydt]で解きたい微分方程式を定義する。
引数は下記の通り。
- var:速度と変位(微分方程式の解)を並べた配列。今回は0番目を\(x\)、1番目を\(y\)、2番目を\(v_{x}=dx/dt\)、3番目を\(v_{y}=dy/dt\)としている。
- t:時間
- m:質点の質量
- g:重力加速度
- mu:抵抗係数
今回解く運動方程式(\ref{rei1-1})を1階の連立常微分方程式で表すと
\begin{align}
\begin{cases}
\displaystyle{\frac{dx}{dt}=v_{x}} \\ \\
\displaystyle{\frac{dy}{dt}=v_{y}} \\ \\
\displaystyle{\frac{dv_{x}}{dt}=-\frac{\mu}{m}v_{x}} \\ \\
\displaystyle{\frac{dv_{y}}{dt}=-\frac{\mu}{m}v_{y}-g}
\end{cases} \tag{2}\label{rei1-2}
\end{align}
となるため、上記4式を定義し、それぞれの左辺、すなわち速度と加速度を返り値とする。
def plot2d(t_list, var_list):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlabel("$x[m]$")
ax.set_ylabel("$y[m]$")
ax.plot(var_list[:, 0], var_list[:, 1])
ax.set_aspect('equal')
plt.show()でグラフを設定する。
var_listは後に定義する、微分方程式の解の配列varを時間ごとに並べた2重配列である。
var_list = [var(t0),var(t1),…] = [[x(t0),y(t0),vx(t0),vy(t0)],[x(t1),y(t1),vx(t1),vy(t1)],…]
グラフにプロットするのはx,yであるため、配列のスライスを利用してvar_listの0番目と1番目を抜き出している。
「ax.set_aspect(‘equal’)」はグラフのx軸、y軸のアスペクト比を同じにするコードである。
if (__name__ == '__main__'):
t_list = np.linspace(0.0, 10, 500)
m = 0.1 #質点の質量[kg]
g = 9.8 #重力加速度[m^2/s]
mu = 1*10**(-3) #抵抗係数[N・s/m]
var_init = [0, 300, 20, 20] #初期値
var_list = odeint(eom, var_init, t_list, args = (m, g, mu))で実際に微分方程式を数値計算する。
「t_list = np.linspace(0.0, 10, 500)」で微分方程式の変数(今回では時間)を定義しており、np.linspace(開始値, 終了値, 刻み幅)である。
今回は0秒から10秒までを刻み幅500で計算する。
「var_init = [0, 300, 20, 20]」は初期値を定義しており、var_init = [x0, y0, v0x, v0y]である。
最後に「var_list = odeint(eom, var_init, t_list, args = (m, g, mu))」で計算を実行する。
引数はそれぞれodeint(解く微分方程式, 初期値, 変数, 微分方程式内の定数)である。
最後に
plot2d(t_list, var_list)でグラフを表示する。
例2:一様磁場中および円筒電場中の荷電粒子
以前に
で紹介した、解析的に解けない微分方程式をodeintモジュールで解いてみる。
上記記事ではデカルト座標系と円筒座標系の2パターンで運動方程式を導出しているので、今回も両パターンで解かせてみる。
まずはデカルト座標系バージョン。
運動方程式は次式のようになる。
\begin{align}
\begin{cases}
\displaystyle{m\frac{d^{2}}{dt^{2}}x=qE\frac{x}{\sqrt{x^{2}+y^{2}}}+qB\frac{d}{dt}y}\\ \\
\displaystyle{m\frac{d^{2}}{dt^{2}}y=qE\frac{y}{\sqrt{x^{2}+y^{2}}}-qB\frac{d}{dt}x}\\ \\
\displaystyle{m\frac{d^{2}}{dt^{2}}z=0}
\end{cases}\tag{3}\label{rei3-1}
\end{align}
上式を1階の連立常微分方程式に書き直すと下式のようになる。
\begin{align}
\begin{cases}
\displaystyle{\frac{dx}{dt}=v_{x}}\\ \\
\displaystyle{\frac{dy}{dt}=v_{y}}\\ \\
\displaystyle{\frac{dz}{dt}=v_{z}} \\ \\
\displaystyle{\frac{dv_{x}}{dt}=\frac{qE}{m}\frac{x}{\sqrt{x^{2}+y^{2}}}+\frac{qB}{m}v_{y}} \\ \\
\displaystyle{\frac{dv_{y}}{dt}=\frac{qE}{m}\frac{y}{\sqrt{x^{2}+y^{2}}}-\frac{qB}{m}v_{x}} \\ \\
\displaystyle{\frac{dv_{z}}{dt}=0}
\end{cases}\tag{4}\label{rei3-2}
\end{align}
実際のプログラム例を下記に示す。
%matplotlib notebook
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#運動方程式
#var[0]=x,var[1]=y,var[2]=z,var[3]=vx,var[4]=vy,var[5]=vz
def eom(var, t, m, q, E, B):
dxdt = var[3]
dydt = var[4]
dzdt = var[5]
dvxdt = (q*E*var[0]/np.sqrt(var[0]**2+var[1]**2)/m)+(q*B*var[4]/m)
dvydt = (q*E*var[1]/np.sqrt(var[0]**2+var[1]**2)/m)-(q*B*var[3]/m)
dvzdt = 0
return [dxdt, dydt, dzdt, dvxdt, dvydt, dvzdt]
#3dグラフ
def plot3d(t_list, var_list):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.set_zlabel("$z$")
ax.plot(var_list[:, 0], var_list[:, 1], var_list[:, 2])
plt.show()
#メイン
if (__name__ == '__main__'):
t_list = np.linspace(0.0, 2, 100000)
m = 9.1093837*10**(-31) #荷電粒子の質量[kg]
q = -1.60217663*10**(-19) #荷電粒子の電荷[C]
E = 5*10**(-9) #電場[V/m]
B = 1*10**(-9) #磁束密度[T]
var_init = [1, 0, 0, 0, 10, 1] #初期値
var_list = odeint(eom, var_init, t_list, args=(m, q, E, B))
#グラフ表示
plot3d(t_list, var_list)これを実行すると下図のグラフが得られる。

続いて円筒座標系バージョン。
運動方程式は下式のようになる。
\begin{align}
\begin{cases}
\displaystyle{m\left(\frac{d}{dt}v_{r}-rv_{\theta}^{2}\right)=q(E+Brv_{\theta})} \\ \\
\displaystyle{m\left(r\frac{d}{dt}v_{\theta}+2v_{r}v_{\theta}\right)=-qBv_{r}} \\ \\
\displaystyle{m\frac{d}{dt}v_{z}=0}
\end{cases}\tag{5}\label{rei3-3}
\end{align}
上式を1階の連立常微分方程式に書き直すと下式のようになる。
\begin{align}
\begin{cases}
\displaystyle{\frac{dr}{dt}=v_{r}} \\ \\
\displaystyle{\frac{d\theta}{dt}=v_{\theta}} \\ \\
\displaystyle{\frac{dz}{dt}=v_{z}} \\ \\
\displaystyle{\frac{dv_{r}}{dt}=rv_{\theta}^{2}+\frac{q}{m}(E+Brv_{\theta})}\\ \\
\displaystyle{\frac{dv_{\theta}}{dt}=-\frac{2v_{r}v_{\theta}}{r}-\frac{qBv_{r}}{mr}}\\ \\
\displaystyle{\frac{dv_{z}}{dt}=0}
\end{cases}\tag{6}\label{rei3-4}
\end{align}
実際のプログラム例を下記に示す。
%matplotlib notebook
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#運動方程式
#var[0]=r,var[1]=theta,var[2]=z,var[3]=vr,var[4]=vtheta,var[5]=vz
def eom(var, t, m, q, E, B):
drdt = var[3]
dthetadt = var[4]
dzdt = var[5]
dvrdt = (var[0]*var[4]**2)+(q*(E+B*var[0]*var[4])/m)
dvthetadt = (-2*var[3]*var[4]/var[0])-(q*B*var[3]/m/var[0])
dvzdt = 0
return [drdt, dthetadt, dzdt, dvrdt, dvthetadt, dvzdt]
#3dグラフ
def plot3d(t_list, var_list):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.set_zlabel("$z$")
ax.plot(var_list[:, 0]*np.cos(var_list[:, 1]), var_list[:, 0]*np.sin(var_list[:, 1]), var_list[:, 2])
plt.show()
#メイン実行部
if (__name__ == '__main__'):
t_list = np.linspace(0.0, 2, 100000)
m = 9.1093837*10**(-31) #荷電粒子の質量[kg]
q = -1.60217663*10**(-19) #荷電粒子の電荷[C]
E = 5*10**(-9) #電場[V/m]
B = 1*10**(-9) #磁束密度[T]
var_init = [1, 0, 0, 0, 10, 1] #初期値
var_list = odeint(eom, var_init, t_list, args=(m, q, E, B))
#グラフ表示
plot3d(t_list, var_list)これを実行すると下図のグラフが得られる。
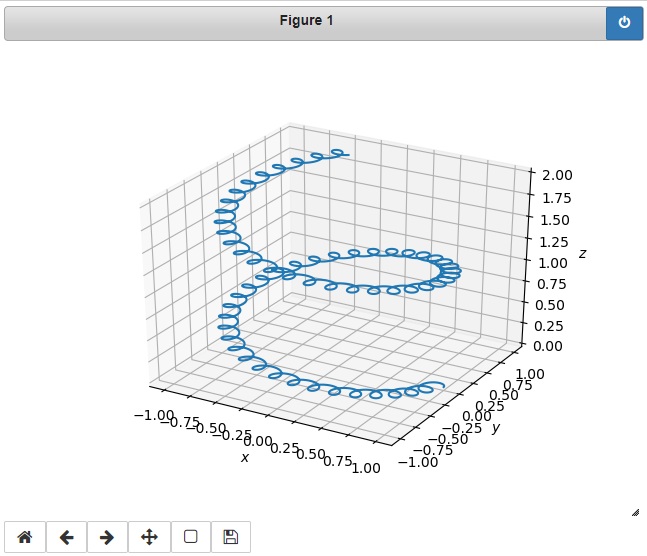
2つのプログラムで初期条件、時間の範囲は同じである。
出力されたグラフが同じであることから、2つの運動方程式(\ref{rei3-1})、(\ref{rei3-3})は同じ運動を記述することがわかる。
終わりに
自分がPythonを初めて触ってから3年が経とうとしているが、その3年の間にPythonでできることの幅がかなり広がっているように感じる。
AI含め今後の発展スピードは更に増していくのだろうが、ただ指を咥えてそれを見守っているだけというのも癪に障る。
食らいつけるだけ食らいつきたいが、どこまで追いかけれれるか…
END





コメント