諸事情で統計力学を復習しているのだが、統計力学に出てくる確率モデルの違いを改めて勉強し直してまとめてみた。
ミクロカノニカル分布
体積\(V\)の中に\(N\)個の同種粒子があり、全系のエネルギー\(U\)で平衡状態にある系を考える。
この系のエネルギー固有状態は既にわかっており、自然数\(i\)でラベリングされているとする。
対応するエネルギー固有値を\(E_{i}\)とする。
ここで十分に小さい量\(\delta>0\)を考え、\(U-\delta V\)と\(U\)の間にほとんどの\(E_{i}\)が収まるとする。
そして、エネルギー固有値\(E_{i}\)が\(U-\delta V<E_{i}\leq U\)を満たすエネルギー固有状態を「許されるエネルギー固有状態」とし、それ以外のエネルギー固有状態は許されない、すなわち出現しないものとする。
そして「許されるエネルギー固有状態」は全て等確率で出現する。
以上をまとめると、エネルギー固有状態\(i\)が出現する確率\(p_{i}^{(\text{MC})}\)は次式のようになる。
\begin{align}
\boxed{
p_{i}^{(\text{MC})}=\begin{cases}
\displaystyle{\frac{1}{W}} &(U-\delta V<E_{i}\leq U)\\ \\
0 & (\text{otherwise})
\end{cases}
}
\end{align}
上式で定まる確率分布をミクロカノニカル分布と呼ぶ。
ただし\(W\)は「許されるエネルギー固有状態」の総数である。
カノニカル分布
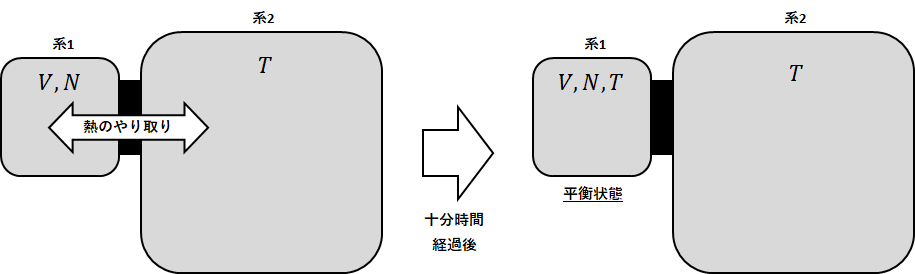
体積\(V\)、粒子数\(N\)の系1が、温度\(T\)の十分大きい系2と接触しており、両者の間では熱のやり取りのみ許されるものとする。
このとき、十分時間が経過すれば系1も温度\(T\)で平衡状態となる。
ミクロカノニカル分布の時と同様に、系1のエネルギー固有状態は既にわかっており、自然数\(i\)でラベリングされ、対応するエネルギー固有値を\(E_{i}\)とする。
このとき、系1がエネルギー固有状態\(i\)をとる確率\(p_{i}^{(\text{C},\beta)}\)
\begin{align}
\boxed{p_{i}^{(\text{C},\beta)}=\frac{e^{-\beta E_{i}}}{Z(\beta)}}
\end{align}
となる。
上式で定まる確率分布をカノニカル分布と呼ぶ。
ただし、\(\beta=1/k_{b}T\)は逆温度であり、
\begin{align}
Z(\beta)=\sum_{i}e^{-\beta E_{i}}
\end{align}
を分配関数と呼ぶ。
グランドカノニカル分布
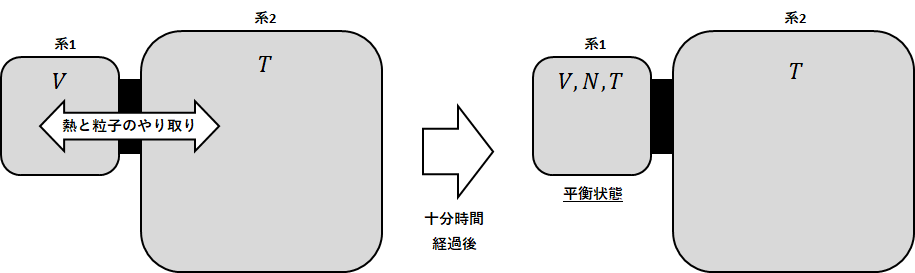
体積\(V\)の系1が、十分な数の粒子を有する温度\(T\)の十分大きい系2と接触しており、両者の間では熱と粒子のやり取りが許され、十分時間が経過して系1が平衡状態になったとする。
カノニカル分布では熱のやり取りしかなかったが、今回は熱に加えて粒子のやり取りもあるということだ。
今回は粒子数も可変パラメータとなるため、エネルギー固有状態をカウントする際に粒子数も考慮する必要がある。
具体的には、系1の粒子数が\(N\)のときの系1のエネルギー固有状態に自然数\(i\)でラベリングしていけばよい。
このとき系1のエネルギー固有状態は\((N,i)\)という2つのパラメータの組み合わせで指定できる。
エネルギー固有状態\((N,i)\)に対応するエネルギー固有値を\(E_{(i,N)}\)とすると、系1がエネルギー固有状態\((N,i)\)をとる確率\(p_{(N,i)}^{(\text{GC},\beta,\mu)}\)は
\begin{align}
\boxed{p_{(N,i)}^{(\text{GC},\beta,\mu)}=\frac{e^{{-\beta E_{(N,i)}+\beta\mu N}}}{N!\,\Xi(\beta,\mu)}}
\end{align}
上式で定まる確率分布をグランドカノニカル分布と呼ぶ。
ただし、\(\beta=1/k_{b}T\)は逆温度、\(\mu\)は化学ポテンシャルであり、
\begin{align}
\Xi(\beta,\mu)=\sum_{N}\frac{1}{N!}\sum_{i}e^{{-\beta E_{(N,i)}+\beta\mu N}}
\end{align}
を大分配関数と呼ぶ。




コメント