前回、
にて水平投射の考え方について解説したので、今回は斜方投射を見ていく。
しかし実際は、水平投射と考え方はほぼ同じである。
2つの運動の組み合わせ
結論から言うと、斜方投射も2つの運動の組み合わせであり、等速直線運動と鉛直投げ上げの組み合わせである。
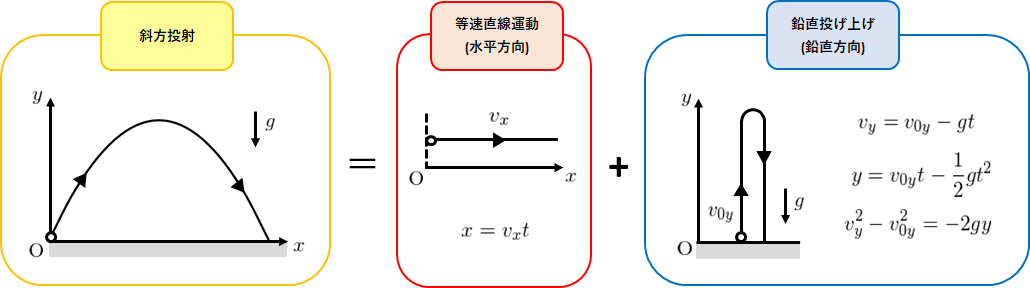
水平投射と同じく、水平方向と鉛直方向で別々に運動を考えて立式し、連立方程式の問題として考えれば大概の問題は解ける。
例題
上記の考え方を念頭に入れた上で、斜方投射の例題を解いてみる。
例題
水平な床に置かれている質点を、水平右向きに初速度\(10\,\text{m/s}\)、鉛直上向きに初速度\(49\,\text{m/s}\)を与えて打ち出す。打ち出した時間を\(0\,\text{s}\)とするとき、次の問いに答えよ。
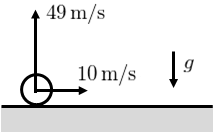
(1) 質点が打ち出されてから水平右向きに\(10\,\text{m}\)進んだとき、質点の鉛直方向の速度\(v_{y}\)、および床からの高さ\(y\)を求めよ。
(2) 質点が床から高さ\(78.4\,\text{m}\)の位置にあるとき、質点の鉛直方向の速度\(v_{y}\)、および質点が水平方向に進んだ距離\(x\)を求めよ。
ただし空気抵抗は無視してよく、重力加速度を\(g=9.8\,\text{m/s}^{2}\)とする。
解説
質点の運動は斜方投射であり、水平方向は等速直線運動、鉛直方向は鉛直投げ上げである。
水平右向き、および鉛直下向きを正にとる。
(1)
質点が水平右向きに\(10\,\text{m}\)進んだときの時間から、質点の鉛直方向の速度\(v_{y}\)、および床からの高さ\(y\)を求める。
質点は水平方向に等速直線運動をするため、
\begin{align}
&x=v_{0x}t \\
&10\,\text{m}=10\,\text{m/s}\cdot t\quad\therefore t=1.0\,\text{s}
\end{align}
となる。
よって求める速度と高さは鉛直投げ上げの式より、
\begin{align}
&v_{y}=v_{0y}-gt=49\,\text{m/s}-9.8\,\text{m/s}^{2}\cdot 1.0\,\text{s}=39.2\,\text{m/s} \quad\therefore\boxed{v_{y}=39.2\,\text{m/s}}\\
&y=v_{0y}t-\frac{1}{2}gt^{2}=49\,\text{m/s}\cdot 1.0\,\text{m/s}-\frac{1}{2}\cdot 9.8\,\text{m/s}^{2}\cdot 1.0^{2}\,\text{m}^{2}/\text{s}^{2}=44.1\,\text{m}\quad\therefore\boxed{y=44.1\,\text{m}}
\end{align}
となる。
(2)
まず、質点の鉛直方向の速度\(v_{y}\)から求める。床からの高さがわかっているので、鉛直投げ上げの式より、
\begin{align}
&v_{y}^{2}-v_{0y}^{2}=-2gy \\
&v_{y}^{2}-49^2\,\text{m}^{2}/\text{s}^{2}=-2\cdot 9.8\,\text{m/s}^{2}\cdot 78.4\,\text{m}\\
&v_{y}^{2}=29.4^{2}\,\text{m}^{2}/\text{s}^{2}\quad\therefore v_{y}=\pm 29.4\,\text{m/s}
\end{align}
となる。
(i) \(v_{y}=29.4\,\text{m/s}\)のとき
鉛直投げ上げの式より、
\begin{align}
&v_{y}=v_{0y}-gt \\
&29.4\,\text{m/s}=49\,\text{m/s}-9.8\,\text{m/s}^{2}\cdot t\quad\therefore t=2.0\,\text{s}
\end{align}
となる。よってこのとき、質点が水平方向に進んだ距離\(x\)は
\begin{align}
x=v_{0x}t=10\,\text{m/s}\cdot 2.0\,\text{s}=20\,\text{m}\quad\therefore x=20\,\text{m}
\end{align}
となる。
(ii) \(v_{y}=-29.4\,\text{m/s}\)のとき
鉛直投げ上げの式より、
\begin{align}
&v_{y}=v_{0y}-gt \\
&-29.4\,\text{m/s}=49\,\text{m/s}-9.8\,\text{m/s}^{2}\cdot t\quad\therefore t=8.0\,\text{s}
\end{align}
となる。よってこのとき、質点が水平方向に進んだ距離\(x\)は
\begin{align}
x=v_{0x}t=10\,\text{m/s}\cdot 8.0\,\text{s}=80\,\text{m}\quad\therefore x=80\,\text{m}
\end{align}
となる。
以上より、求める速度と距離は\(\boxed{v_{y}=29.4\,\text{m/s},\,x=20\,\text{m}}\)および\(\boxed{v_{y}=-29.4\,\text{m/s},\,x=80\,\text{m}}\)となる。
チャンレンジ問題
ここで、上の例題よりも難易度が高いチャレンジ問題を出題する。
余裕がある人は解いてみてほしい。
チャレンジ問題
水平な床に質点が置かれており、質点から水平右向きに距離\(7.5\,\text{m}\)だけ離れた地点を起点として幅\(2.5\,\text{m}\)の穴があいている。質点に初速度を与えて斜方投射させ、この穴に入れたい。質点の初速度を\(v_{0}\)、床に対する投射角度を\(\theta\)とするとき、次の問いに答えよ。
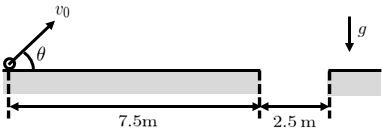
(1) 床に対する投射角度が\(\theta=\pi/12\)で固定されているとき、質点を穴に入れることができる初速度\(v_{0}\)の範囲を求めよ。
(2) 質点の初速度が\(v_{0}=14\,\text{m/s}\)で固定されているとき、質点を穴に入れることができる\(\sin 2\theta\)の範囲を求めよ。
ただし質点の大きさと空気抵抗は無視してよく、重力加速度を\(g=9.8\,\text{m/s}\)とする。
解説
質点の発射位置を原点とし、質点を発射した時間を\(t=0\)とする。
質点が斜方投射され、再び床と同じ高さに到達した際に穴に入っていれば良い。
質点の鉛直方向の位置が床と同じ高さ\(y=0\)となる時間\(t\)は、鉛直方向の初速度を\(v_{0y}\)とすると、斜方投射の式より、
\begin{align}
&y=v_{0y}t-\frac{1}{2}gt^{2}\\
&0=v_{0}\sin\theta\,t-\frac{1}{2}gt^{2}\quad \therefore t=0,\frac{2v_{0}\sin\theta}{g}
\end{align}
となる。
投射後に再び\(y=0\)となる時間は\(t=2v_{0}\sin\theta/g\)であるため、この時間での水平方向の位置\(x\)は水平方向の初速度を\(v_{0x}\)として
\begin{align}
x=v_{0x}t=v_{0}\cos\theta\frac{2v_{0}\sin\theta}{g}=\frac{v_{0}^{2}\sin 2\theta}{g}
\end{align}
となる。
よって
\begin{align}
7.5\,\text{m}\le \frac{v_{0}^{2}\sin 2\theta}{g}\le 10\,\text{m}
\end{align}
の範囲内であれば質点が穴に入るため、後はここに具体的に値を入れていけばよい。
(1)
投射角度が\(\theta=\pi/12\)で固定されているため、
\begin{gather}
7.5\,\text{m}\le \frac{v_{0}^{2}\sin 2\theta}{g}\le 10\,\text{m}\\
7.5\,\text{m}\le \frac{v_{0}^{2}\sin (\pi/6)}{9.8\,\text{m/s}^{2}}\le 10\,\text{m}\\
2\cdot 7.5\,\text{m}\cdot 9.8\,\text{m/s}^{2}\le v_{0}^{2}\le 2\cdot 10\,\text{m}\cdot 9.8\,\text{m/s}^{2}\\
49\cdot 3 \,\text{m}^{2}/\text{s}^{2}\le v_{0}^{2}\le 196\,\text{m}^{2}/\text{s}^{2}\\
\therefore \boxed{7\sqrt{3}\,\text{m/s}\le v_{0}\le 14\,\text{m/s}}
\end{gather}
となる。
(2)
初速度が\(v_{0}=14\,\text{m/s}\)で固定されているため、
\begin{gather}
7.5\,\text{m}\le \frac{v_{0}^{2}\sin 2\theta}{g}\le 10\,\text{m}\\
7.5\,\text{m}\le \frac{14^{2}\,\text{m}^{2}/\text{s}^{2}\sin 2\theta}{9.8\,\text{m/s}^{2}}\le 10\,\text{m}\\
\frac{7.5\,\text{m}\cdot 9.8\,\text{m/s}^{2}}{14^{2}\,\text{m}^{2}/\text{s}^{2}}\le\sin 2\theta\le\frac{10\,\text{m}\cdot 9.8\,\text{m/s}^{2}}{14^{2}\,\text{m}^{2}/\text{s}^{2}}\\
\therefore\boxed{\frac{3}{8}\le \sin 2\theta\le\frac{1}{2}}
\end{gather}
となる。
終わりに
問題作るのって時間かかるけど結構面白い。
著作権の問題が無ければ過去に解いた面白い問題をそのまま載せたいところだが…
END





コメント